Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\frac{{x - 1}}{{x + 1}}\;\)xác định khi \(x + 1 \ne 0 \Leftrightarrow x \ne - 1\)
\(\frac{{x - 1}}{{x + 1}} = 0 \Leftrightarrow x - 1 = 0 \Leftrightarrow x = 1\;\)
Tập nghiệm của phương trình là \({S_1} = \left\{ 1 \right\}\)
\({x^2} - 1 = 0 \Leftrightarrow {x^2} = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = - 1}\end{array}} \right.\;\)
Tập nghiệm của phương trình là \({S_2} = \left\{ {1; - 1} \right\}\)
Vậy tập nghiệm của 2 phương trình là không tương đương nhau

Đáp án D
Ta có
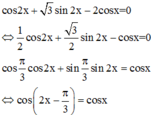
Do đó để phương trình ![]() tương đương với phương trình
tương đương với phương trình
![]()

Đáp án D
Dùng công thức cos a.cos b+ sin a. sin b= cos (a-b) để biến đổi phương trình không chứa
α
về dạng giống phương trình có chứa
α
Ta có

a) Phương trình: \({x^2} - 3x + 2 = 0\,\,\,\left( 1 \right)\)
Ta có: \(\Delta = 9 - 4.2 = 1 > 0\)
Phương trình (1) có hai nghiệm \(\left\{ \begin{array}{l}{x_1} = \frac{{3 + 1}}{{2.1}} = 2\\{x_1} = \frac{{3 - 1}}{{2.1}} = 1\end{array} \right.\) => \({S_1} = \left\{ {1;2} \right\}\)
Phương trình: \(\left( {x - 1} \right)\left( {x - 2} \right) = 0\,\,\,\left( 2 \right)\)\( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\) => \({S_2} = \left\{ {1;2} \right\}\)
b) Hai tập \({S_1};{S_2}\) có bằng nhau

Ta có:
\(f'\left(x\right)=6x^2-2x\\ g'\left(x\right)=3x^2+x\)
Theo đề bài, ta có:
\(f'\left(x\right)>g'\left(x\right)\\ \Leftrightarrow6x^2-2x>3x^2+x\\ \Leftrightarrow3x^2-3x>0\\ \Leftrightarrow3x\left(x-1\right)>0\\ \Leftrightarrow\left[{}\begin{matrix}x>1\\x< 0\end{matrix}\right.\)
Vậy tập nghiệm của bất phương trình là \(\left(-\infty;0\right)\cup\left(1;+\infty\right)\)
Chọn D.

\(\Leftrightarrow\frac{\sqrt{3}}{2}sinx-\frac{1}{2}cosx=\frac{1}{2}\)
\(\Leftrightarrow sinx.cos\left(\frac{\pi}{6}\right)-cosx.sin\left(\frac{\pi}{6}\right)=\frac{1}{2}\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{6}\right)=\frac{1}{2}\)
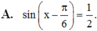
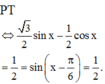
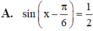
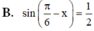
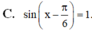

Hai phương trình \(x - 1 = 0\)và \(\frac{{{x^2} - 1}}{{x + 1}} = 0\) có tương đương vì:
\(\begin{array}{l}\frac{{{x^2} - 1}}{{x + 1}} = 0\\ \Leftrightarrow \frac{{\left( {x - 1} \right).\left( {x + 1} \right)}}{{x + 1}} = 0\\ \Leftrightarrow x - 1 = 0\end{array}\)