
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Gọi số đo góc C là x (độ) (0<x<70). => Số đo góc B là x + 40 (độ).
Tổng 3 góc trong 1 tam giác là 180 độ. => Số đo góc A là 180 - (x + 40) - x = 140 - 2x (độ).
AM phân giác góc BAC. => Số đo góc BAM = Số đo góc CAM = (140 - 2x) : 2 = 70 - x (độ).
Tổng 3 góc trong tam giác AMC là 180 độ. => Số đo góc AMC = 180 - Số đo góc CAM - Số đo góc C = 180 - (70 - x) - x = 110 (độ).
Đáp số: Số đo góc AMC = 110 độ.
b) D là trung điểm BC, ED vuông góc với BC. => Tam giác EBC cân tại E. => Số đo góc EBC = Số đo góc ECB = x (độ).
Mà số đo góc ABC là (x + 40) (độ). => Số đo góc ABE = Số đo góc ABC - Số đo góc EBC = (x + 40) - x = 40 (độ).
Đáp số: Số đo góc ABE = 40 độ.
A B C M D E

Đáp án:C
Giải thích các bước giải:
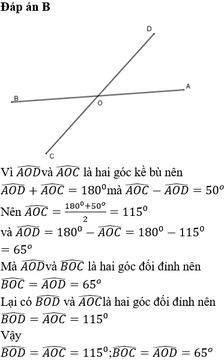
Ta có: góc xby = góc zby = 70 độ (2 góc đối đỉnh)

a.Ta có: OD=OB+BD
OC=OA+AC
mà OA=OB; AC=BD
=>OD=OC
Xét 2 TG ODA và OCB;ta có:
OA-OB(gt); O:góc chung; OD=OC(cmt)
=>TG ODA= TG OCB(c.g.c)
=>AD=BC(2 cạnh tương ứng)
b. TG ODA=TG OCB=> góc C=góc D(2 góc tương ứng)
=>OAD=OBC(2 góc tương ứng)
Ta có: OAD+EAC=180o(kề bù) (1)
OBC+EBD=180o(kề bù) (2)
Từ (1) và (2)=> OAD+EAC=OBC+EBD=180o
mà OAD=OBC(cmt)=>EAC=EBD
Xét 2 TG EAC và EBD; ta có:
AC=BD(gt); C=D(cmt); EAC=EBD(cmt)
=>TG EAC=TG EBD (g.c.g)

trả lời:\
Vì Ax//By;C,E thuộc Ax;D,F thuộc By=>Ac//BD, AE//BF
=>góc CAO=góc OBD
Góc AEO=góc OFD
Góc ACO= góc ODB
xét tam giác ACO và tam giác OBD ta có
OA=OB;Góc CAO=BOD;ACO=ODB
=>hai tam giác này bằng nhau
=>góc COA=BOD(2 góc tương ứng )
Mà A,O,B thửng hàng=>góc COB+COA=180 độ
=>góc BOD+COB=180 độ
=>O,C,D thẳng hàng
tương tự chứng minh với E,O,F
b,Từ những tam giác bằng nhau ta có được OE=OF;CO=OD
xét tam giác OED và OCF có OE=OF; CO=OD; góc COF=EOD( 2 góc đối đỉnh)
=>góc FOD=CDE; DE=CF(2 cạnh tương ứng)
mà hai góc này ở vị trí so le trong của hai đoạn thẳng DE và CF được cắt bởi đoạn DC
=>DE//CF
học tốt

#)Giải :
A B C I D E
Ta có : \(\hept{\begin{cases}\widehat{DIB}=\widehat{IBC}\left(slt\right)\\\widehat{DBI}=\widehat{IBC}\left(p/gBI\right)\end{cases}\Rightarrow\widehat{DIB}=\widehat{DBI}}\)
\(\Rightarrow\Delta BID\) cân tại D \(\Rightarrow BI=ID\) (1)
Lại có : \(\hept{\begin{cases}\widehat{EIC}=\widehat{BCI}\left(slt\right)\\\widehat{ECI}=\widehat{BCI\left(p/gCI\right)}\end{cases}\Rightarrow\widehat{EIC}=\widehat{ECI}}\)
\(\Rightarrow\Delta CIE\) cân tại E \(\Rightarrow IE=EC\) (2)
Từ (1) và (2) \(\Rightarrowđpcm\)
A B C O D E 1 2 1 2 1 2
cm: Ta có: OD // BC => \(\widehat{O_1}=\widehat{B_2}\) (so le trong) mà \(\widehat{B_1}=\widehat{B_2}\) (gt)
=> \(\widehat{O_1}=\widehat{B_1}\) => t/giác OBD cân tại D => DB = DO
OE // BC => \(\widehat{O_2}=\widehat{C_2}\)(so le trong) mà \(\widehat{C_1}=\widehat{C_2}\) (gt)
=> \(\widehat{O_2}=\widehat{C_1}\) => t/giác OEC cân tại E => OE = EC
Ta lại có:DE = OD + DE (O \(\in\)DE)
hay DE = DB + EC (đpcm)