Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn: A
Hướng dẫn:
- Điểm M nằm trên đường thẳng nối hai điện tích và cách q 1 một khoảng r 1 = 5 (cm) = 0.05 (m); cách q 2 một khoảng r 2 = 15 (cm) = 0,15 (m). Điểm M nằm ngoài khoảng q 1 q 2 .
- Cường độ điện trường do điện tích q 1 = 5 . 10 - 9 (C) gây ra tại M có độ lớn E 1 = 9 .10 9 q 1 r 1 2 = 18000 (V/m), có hướng ra xa điện tích q 1 .
- Cường độ điện trường do điện tích q 2 = - 5 . 10 - 9 (C) gây ra tại M có độ lớn E 2 = 9 .10 9 q 2 r 2 2 = 2000 (V/m), có hướng về phía q 2 .
![]()
- Cường độ điện trường tổng hợp tại điểm M là
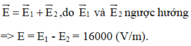

Chọn: B
Hướng dẫn:
- Điểm M nằm trên đường thẳng nối hai điện tích và cách đều hai điện tích, điểm đó cách mỗi điện tích một khoảng r = 5 (cm) = 0,05 (m).
- Cường độ điện trường do điện tích q 1 = 5 . 10 - 9 (C) gây ra tại M có độ lớn E 1 = 9 .10 9 q 1 r 2 = 18000 (V/m), có hướng ra xa điện tích q 1 .
- Cường độ điện trường do điện tích q 2 = - 5 . 10 - 9 (C) gây ra tại M có độ lớn E 2 = 9 .10 9 q 2 r 2 = 18000 (V/m), có hướng về phía q 2 tức là ra xa điện tích q 1 .
![]()
- Cường độ điện trường tổng hợp tại điểm M là
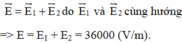

Chọn D.
Điểm nằm trên đường thẳng đi qua vị trí đi qua hai điện tích là trung điểm của q1 và q2


Ta có AM = BM = A H 2 + H M 2 = 9 2 + 12 2 = 15 (cm)
Các điện tích q 1 v à q 2 gây ra tại M các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ:
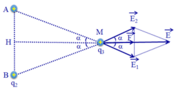
Có độ lớn: E 1 = E 2 = k | q 1 | A M 2 = 9.10 9 .6.10 − 6 0 , 15 2 = 24 . 10 5 (V/m).
Cường độ điện trường tổng hợp tại M là: E → = E 1 → + E 2 → .
Có phương chiều như hình vẽ, có độ lớn:
E = E 1 cos α + E 2 cos α = 2 E 1 cos α
= 2 E 1 . H M A M = 2 . 24 . 10 5 . 12 15 = 38 , 4 . 10 5 (V/m).
F → = q 3 . E → ; vì q 3 > 0 nên F → cùng phương ngược chiều với E → và có độ lớn:
F = q 3 . E = 5 . 10 - 8 . 38 , 4 . 10 5 = 0 , 192 ( N )

a/ \(F=\dfrac{k\left|q_1q_2\right|}{r^2}=\dfrac{9.10^9.5.10^{-7}.8.10^{-7}}{0,2^2}=...\left(N\right)\)
b/ \(\left|q_1\right|< \left|q_2\right|\Rightarrow\) C gần q1 hơn
\(\Rightarrow\dfrac{k\left|q_1\right|}{AC^2}=\dfrac{k\left|q_2\right|}{\left(AB+AC\right)^2}\Leftrightarrow\dfrac{5}{AC^2}=\dfrac{8}{\left(0,2+AC\right)^2}\Rightarrow AC=...\left(m\right)\)

