Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi x là vận tốc ve máy
y là vận tốc otô
theo đề bài ta có hpt
120/x=80/y và 144/x-1=56/y
giải hpt ta được
x=60
y=40
vậy vận tốc xe máy là 60km/h
vận tốc oto là 40km/h
Tick nhé

Đáp án D
Gọi vận tốc của ô tô là x (km/h)
Vận tốc của xe máy là y (km/h) ( Điều kiện: x > y > 0, x > 10)
Ta có vận tốc của ô tô lớn hơn vận tốc của xe máy 10 km/h nên : x – y = 10 (1)
Sau 2 giờ ô tô đi được quãng đường là 2x (km)
Sau 2 giờ xe máy đi được quãng đường là: 2y (km)
Sau 2 giờ thì chúng gặp nhau, ta có phương trình: 2x + 2y = 180 hay x + y = 90 (2)
Từ (1), (2) ta có hệ phương trình :
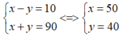
Thỏa mãn điều kiện,vậy vận tốc của ô tô là 50 km/h và vận tốc của xe máy là: 40 km/h

Gọi v xe máy là x ( km/h)
" " ô tô là y (km/h)
Quãng đg của xe máy khi khi cùng khởi hành là 120 km
Quãng đg của ô tô khi cùng khởi hành là 200 - 120 =80 km
t xe máy là 120/x (9giờ )
t ô tô là 80/y ( giờ )
-Vì 2 xe c` xuất phát và cũng cùng gặp nhau nên t gian đi của 2 xe = nhau => phương trình
120/x =80/y (1)
Xe máy khi khởi hành sau thì sẽ đi chậm hơn => Quãng đg xe máy đi được là 200 - 24=96 km
Và cũng suy ra đk quãng đg ô tô đi là 200 - 96 =104 km
t xe máy khi khởi hành sau là 96/x (giờ )
t ô tô khi khởi hành trc là 104/y ( giờ )
- Vì xe máy đi sau 1 h nên ta có pt 104/y +-1 = 96/x (2)
Đấy xong là từ (1) và (2) => hệ pt
{120/x=80/y
{104/y-1=96/x
=>{y=40
{x=60
chúc bn hok tốt

Gọi vận tốc của xe máy là x ; vận tốc của ô tô là y ( x, y >0, km/h)
+) Hai xe khởi hành cùng 1 lúc gặp nhau tại C cách A 120 km => C cách B : 200 - 120 = 80 km
=> Thời gian xe máy đi được: \(\frac{120}{x}\)(h)
Thời gian ô tô đi được là: \(\frac{80}{y}\)(h)
Vì hai xe xuất phát cùng 1 nên thời gian đi được của hai xe bằng nhau
do đó: \(\frac{120}{x}=\frac{80}{y}\)<=> \(120.\frac{1}{x}-80.\frac{1}{y}=0\)(1)
+) Xe máy khởi hành sau ô tô 1 giờ:
Vì xe máy khởi hành sau nên D sẽ cách A 120 - 24 = 96 (km) và D cách B : 80 + 24 = 104 (km)
=> Thời gian xe máy đi được là: \(\frac{96}{x}\)(h)
Thời gian ô tô đi được là: \(\frac{104}{y}\)(h)
Do đó: \(\frac{96}{x}+1=\frac{104}{y}\)
<=> \(96.\frac{1}{x}-104.\frac{1}{y}=-1\)(2)
Từ (1); (2) => \(\hept{\begin{cases}\frac{1}{x}=\frac{1}{60}\\\frac{1}{y}=\frac{1}{40}\end{cases}}\)<=> \(\hept{\begin{cases}x=60\\y=40\end{cases}}\)
Vậy vận tốc xe máy là 60km/h; vận tốc ô tô là 40 km/h

Gọi vận tốc của xe máy và ô tô lần lượt là: x,y (km/h) (x,y>0)
Khi khởi hành cùng lúc, quãng đường xe máy đi được đến khi gặp nhau là: 120 (km)
Khi khởi hành cùng lúc, thời gian xe máy đi được đến khi gặp nhau là: \(\frac{120}{x}\left(h\right)\)
Khi khởi hành cùng lúc, quãng đường ô tô đi được đến khi gặp nhau là:
200-120=80 (km)
Khi khởi hành cùng lúc, thời gian ô tô đi được đến khi gặp nhau là: \(\frac{80}{y}\left(h\right)\)
Vì 2 xe khởi hành cùng lúc nên đến khi gặp nhau 2 xe trong khoảng thời gian như nhau nên :
\(\frac{120}{x}=\frac{80}{y}\left(1\right)\)
Khi xe máy khởi hành sau 1 giờ, quãng đường xe máy đi được đến khi gặp nhau là:
120-24=96 (km)
Khi xe máy khởi hành sau 1 giờ, thời xe máy đi được đến khi gặp nhau là: \(\frac{96}{x}\left(h\right)\)
Khi xe máy khởi hành sau 1 giờ, quãng đường ô tô đi được đến khi gặp nhau là:
200-96=104 (km)
Khi xe máy khởi hành sau 1 giờ, thời ô tô đi được đến khi gặp nhau là:\(\frac{104}{y}\left(h\right)\)
Vì xe máy khởi hành sau 1 giờ nên ta có :
\(\frac{96}{x}=\frac{104}{y}-1\left(2\right)\)
Ta có hệ phương trình:
\(\hept{\begin{cases}\frac{120}{x}=\frac{80}{y}\\\frac{96}{x}=\frac{104}{y}-1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{1}{x}=\frac{80}{120y}=\frac{2}{3y}\\96.\frac{2}{3y}=\frac{104-y}{y}\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}\frac{1}{x}=\frac{2}{3y}\\\frac{64}{y}=\frac{104-y}{y}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{1}{x}=\frac{2}{3y}\Rightarrow x=1:\frac{2}{120}=60\\y=104-64=40\end{cases}}\)
Vậy vận tốc của xe máy là 60km/h và vận tốc của ô tô là 40km/h.
Gọi vận tốc xe máy là x(km/h)
(ĐK: x>0)
Vận tốc xe ô tô là x+20(km/h)
CB=AB-AC=80km
Thời gian ô tô đi từ B đến chỗ gặp là \(\dfrac{80}{x+20}\left(giờ\right)\)
Thời gian xe máy đi từ A đến chỗ gặp là \(\dfrac{120}{x}\left(giờ\right)\)
Do đó, ta có phương trình:
\(\dfrac{80}{x+20}=\dfrac{120}{x}\)
=>\(\dfrac{2}{x+20}=\dfrac{3}{x}\)
=>3(x+20)=2x
=>3x+60=2x
=>x=-60
=>Đề sai rồi bạn