Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điện trở của dây thứ nhất là:
\(R_1=\rho\dfrac{l_1}{S_1}\)
Điện trở của dây thứ hai là:
\(R_2=\rho\dfrac{l_2}{S_2}=\rho\dfrac{2l_1}{2S_1}=\rho\dfrac{l_1}{S_1}=R_1\)
Vậy điện trở của hai dây dẫn này là như nhau

Chọn C. 4 lần
Do dây thứ nhất dài hơn dây thứ hai 8 lần và có tiết diện lớn gấp 2 lần so với dây thứ hai. Chiều dài lớn hơn 8 lần nên điện trở lớn hơn 8 lần, tiết diện lớn gấp 2 lần nên điện trở giảm đi 2 lần. Vì vậy dây thứ nhất có điện trở lớn gấp 4 lần dây thứ hai.

Áp dụng công thức: 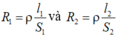 (hai dây này cùng làm bằng một loại vật liệu)
(hai dây này cùng làm bằng một loại vật liệu)
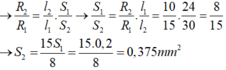

\(=>\dfrac{R1}{R2}=\dfrac{\dfrac{pl1}{S1}}{\dfrac{pl2}{S2}}=\dfrac{l1.S2}{l2.S1}=\dfrac{l1.4S1}{2l1.S1}=2\)
\(=>\dfrac{R1}{R2}=2=>R2=\dfrac{R1}{2}=\dfrac{6}{2}=3\left(ôm\right)\)

Điện trở dây thứ nhất: \(R_1=\rho\cdot\dfrac{l_1}{S_1}=8\Omega\)
Điện trở dây thứ 2: \(R_2=\rho\cdot\dfrac{l_2}{S_2}=\rho\cdot\dfrac{l_1}{2}:2S_1=\rho\cdot\dfrac{l_1}{4S_1}=\dfrac{1}{4}R_1\)
\(\Rightarrow R_2=\dfrac{1}{4}\cdot8=2\Omega\)

Điện trở dây thứ nhất: \(R_1=p.\dfrac{l1}{S1}=8\)Ω
Điện trở dây thứ2: \(R_2=p.\dfrac{l2}{S2}=p.\dfrac{l1}{2}:2S1=p.\dfrac{l1}{4S1}=\dfrac{1}{4}R_1\)
⇒R2=\(\dfrac{1}{4}\)⋅8=2Ω
Ta có 2 dây dẫn được làm từ cùng một chất
\(\Rightarrow\dfrac{R_1}{R_2}=\dfrac{\dfrac{l_1}{S_1}}{\dfrac{l_2}{S_2}}\)\(\Rightarrow\dfrac{8}{R_2}=\dfrac{\dfrac{2l_2}{S_1}}{\dfrac{l_2}{2S_1}}=\dfrac{2l_2}{S_1}.\dfrac{2S_1}{l_2}=4\)
\(\Rightarrow R_2=\dfrac{8}{4}=2\left(\Omega\right)\)

+) Dây thứ nhất có đường kính tiết diện d 1 = 0,5mm, suy ra tiết diện là:
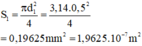
+) Dây thứ hai có đường kính tiết diện d 2 = 0,3mm, suy ra tiết diện là:
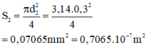
Lập tỉ lệ:
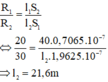

Chọn A. Các dây dẫn này phải có cùng tiết diện, được làm từ cùng một vật liệu, nhưng có chiều dài khác nhau

Chọn B. Các dây dẫn này phải có cùng chiều dài, được làm từ cùng một vật liệu, nhưng có tiết diện khác nhau.
\(\dfrac{R_1}{R_2}=\dfrac{S_2}{S_1}=\dfrac{S_2}{2S_2}=\dfrac{1}{2}\Rightarrow R_2=\dfrac{1}{2}R_1\)
Vậy điện trở dây 1 gấp 2 lần điện trở dây dẫn 2