Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức tính năng lượng dao động của con lắc đơn ta có:
\(W_1 = \dfrac{1}{2}.m_1.g.\ell_1. \alpha_1 ^{2}\) và \(W_2 = \dfrac{1}{2}.m_2.g.\ell_2. \alpha_2 ^{2}\)
Theo giả thiết hai con lắc đơn có cùng năng lượng
\(\Rightarrow \dfrac{1}{2}.m_1.g.\ell_1. \alpha_1 ^{2}=\dfrac{1}{2}.m_2.g.\ell_2. \alpha_2 ^{2}\)
Do khối lượng hai con lắc bằng nhau nên:
\(\ell_1.\alpha_1 ^{2} = \ell_2. \alpha_2 ^{2}\)
\(\Rightarrow \alpha_2 = \alpha_1 .\sqrt{l1/l2}\).
Thay số ta tìm được: \(\alpha_2 = 5,625^0\)

\(T_1=\frac{\Delta t}{40}.\)
\(T_2=\frac{\Delta t}{39}.\)
=> \(\frac{T_1}{T_2}=\frac{40}{39}=\sqrt{\frac{l_1}{l_2}}\).
Khi cho quả cầu tích điện và đặt điện trường vào thì gia tốc biểu kiến của con lắc lúc này là \(\overrightarrow{g_{bk}}=\overrightarrow{g}+\frac{\overrightarrow{F_đ}}{m}=\overrightarrow{g}+\frac{\overrightarrow{E}q}{m}\)
Do để chu kì không đổi khi tăng chiều dài thì g cũng phải tăng như vậy \(g_{bk}=g+\frac{E}{m}=g+\frac{Eq}{m}\)
Để \(T_1=T_2\)
=>\(2\pi\sqrt{\frac{l_2}{g_{bk}}}=2\pi\sqrt{\frac{l_1}{g}}\)
=> \(\frac{l_2}{l_1}=\frac{g+\frac{Eq}{m}}{g}=\frac{40^2}{39^2}.\)
=> \(E=2,08.10^4V.\)

Đáp án B
Trong cùng một khoảng thời gian t, con lắc thứ nhất thực hiện được 60 dao động toàn phần còn con lắc kia thực hiện được 50 dao động toàn phần. Biết chiều dài dây treo của chúng khác nhau một đoạn 44 cm. Gọi chiều dài của con lắc có dây treo ngắn hơn là l1 và chiều dài của con lắc đơn kia là l2
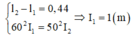

Chọn đáp án B
Trong cùng một khoảng thời gian t, con lắc thứ nhất thực hiện được 60 dao động toàn phần còn con lắc kia thực hiện được 50 dao động toàn phần. Biết chiều dài dây treo của chúng khác nhau một đoạn 44 cm. Gọi chiều dài của con lắc có dây treo ngắn hơn là I 1 và chiều dài của con lắc đơn kia là I 2 : I 2 - I 1 = 0 , 44 60 2 I 1 = 50 2 I 2 ⇒ I 1 = 1 m
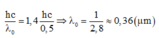

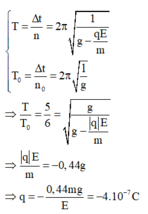

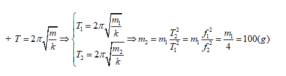
C vì số dao động không phụ thuộc vào khối lượng