K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
15 tháng 9 2021
1.
\(sin\left(x-\dfrac{\pi}{3}\right)\in\left[-1;1\right]\)
\(\Rightarrow y=2sin\left(x-\dfrac{\pi}{3}\right)+3\in\left[1;5\right]\)
\(\Rightarrow\left\{{}\begin{matrix}y_{min}=1\\y_{max}=5\end{matrix}\right.\)
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
\(y=2-2.\left(2sinx.cosx\right)=2-2sin2x\)
Do \(-1\le sin2x\le1\Rightarrow0\le y\le4\)
\(y_{min}=0\) khi \(sin2x=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
\(y_{max}=4\) khi \(sin2x=-1\Rightarrow x=-\dfrac{\pi}{4}+k\pi\)
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
\(y=2\left(1-cos2x\right)-cos2x=2-3cos2x\)
Do \(-1\le cos2x\le1\Rightarrow-1\le y\le5\)
\(y_{min}=-1\) khi \(cos2x=1\Leftrightarrow x=k\pi\)
\(y_{max}=5\) khi \(cos2x=-1\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
ĐKXĐ: \(cos2x\ge0\Rightarrow0\le cos2x\le1\)
\(\Rightarrow3.0+1\le y\le3.\sqrt{1}+1\)
\(\Rightarrow1\le y\le4\)
\(y_{min}=1\) khi \(cos2x=0\Rightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
\(y_{max}=4\) khi \(cos2x=1\Rightarrow x=k\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 9 2020
8.
\(y=cos^2x+2\left(2cos^2x-1\right)=5cos^2x-2\)
Do \(0\le cos^2x\le1\Rightarrow-2\le y\le3\)
\(y_{min}=-2;y_{max}=3\)
10.
\(y=2-\left(cosx+1\right)^2\le2\)
\(y_{max}=2\)
14.
Hàm tuần hoàn với chu kì \(T=\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 10 2020
1.
\(\Leftrightarrow cosx=\frac{\sqrt{3}}{2}\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=-\frac{\pi}{6}+n2\pi\end{matrix}\right.\)
Do \(0< x< 2\pi\Rightarrow\left\{{}\begin{matrix}0< \frac{\pi}{6}+k2\pi< 2\pi\\0< -\frac{\pi}{6}+n2\pi< 2\pi\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-\frac{1}{12}< k< \frac{11}{12}\\\frac{1}{12}< n< \frac{13}{12}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=0\\n=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}\\x=\frac{11\pi}{6}\end{matrix}\right.\) \(\Rightarrow\sum x=\frac{\pi}{6}+\frac{11\pi}{6}=2\pi\)
2.
\(-\frac{\pi}{4}\le x\le\frac{\pi}{3}\Rightarrow-\frac{\sqrt{2}}{2}\le sinx\le\frac{\sqrt{3}}{2}\)
\(\Rightarrow0\le\left|sinx\right|\le\frac{\sqrt{3}}{2}\)
\(y_{max}=\frac{\sqrt{3}}{2}\) khi \(x=\frac{\pi}{3}\)
\(y_{min}=0\) khi \(x=0\)
NL
2
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y=4\left(1-sin^2x\right)+2sinx+2=-4sin^2x+2sinx+6\)
Đặt \(sinx=t\in\left[-1;1\right]\Rightarrow y=f\left(t\right)=-4t^2+2t+6\)
\(-\dfrac{b}{2a}=\dfrac{1}{4}\in\left[-1;1\right]\)
\(f\left(-1\right)=0\) ; \(f\left(\dfrac{1}{4}\right)=\dfrac{25}{4}\); \(f\left(1\right)=4\)
\(\Rightarrow y_{max}=\dfrac{25}{4}\) khi \(sinx=\dfrac{1}{4}\)
\(y_{min}=0\) khi \(sinx=-1\)
1 tháng 11 2021
Ta có: \(y=4cos^2x+2sinx+2=4-4sin^2x+2sinx+2=-4sin^2x+2sinx+6=-\left(4sin^2x-2sinx+\dfrac{1}{16}-\dfrac{1}{16}-6\right)=-\left(2sin^2x-\dfrac{1}{4}\right)^2+\dfrac{97}{16}\)
Ta có: \(-\left(2sin^2x-\dfrac{1}{4}\right)^2\le0\Rightarrow y\le\dfrac{97}{16}\)
Vậy \(y_{max}=\dfrac{97}{16}\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 9 2020
2.
\(0\le\left|sinx\right|\le1\Rightarrow1\le y\le3\)
Min và max lần lượt là 3 và 1
3.
\(cos\left(x-\frac{\pi}{2}\right)\le1\Rightarrow y\le3.1+1=4\)
8.
\(y=\frac{1}{2}+\frac{1}{2}cos2x+2cos2x=\frac{1}{2}+\frac{5}{2}cos2x\le\frac{1}{2}+\frac{5}{2}.1=3\)
15.
Nó đi qua vô số điểm nên ko có 4 đáp án để chọn thì ko ai có thể trả lời câu này cho bạn cả
18.
\(y=\frac{sinx+2cosx+1}{sinx+cosx+2}\Leftrightarrow y.sinx+y.cosx+2y=sinx+2cosx+1\)
\(\Leftrightarrow\left(y-1\right)sinx+\left(y-2\right)cosx=1-2y\)
\(\left(y-1\right)^2+\left(y-2\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow2y^2+2y-4\le0\Rightarrow-2\le y\le1\)
\(\Rightarrow y_{max}=1\)
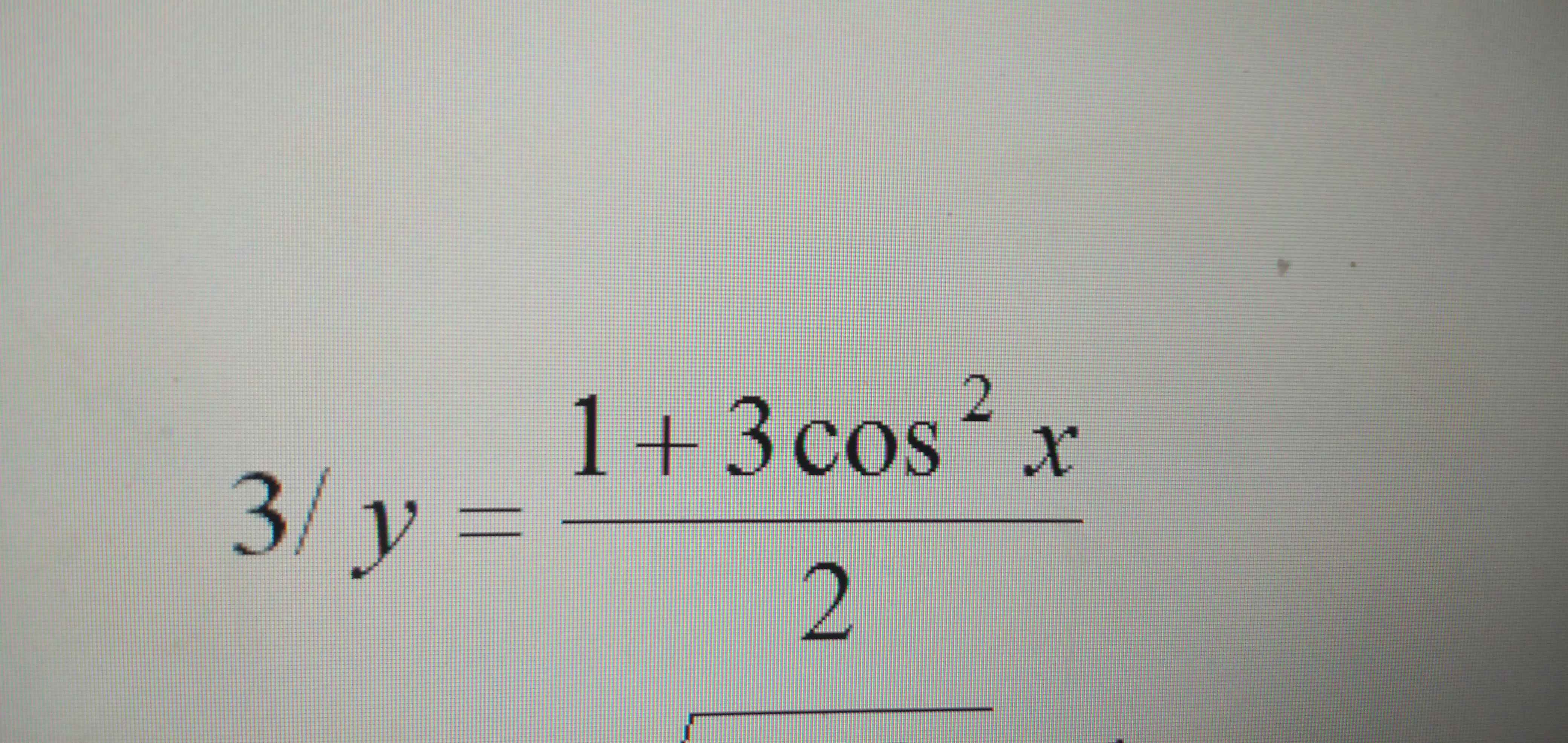
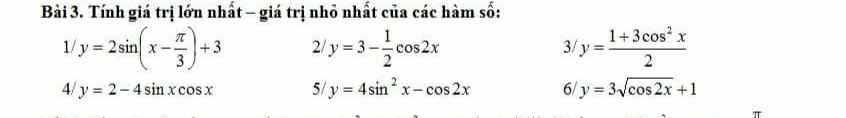
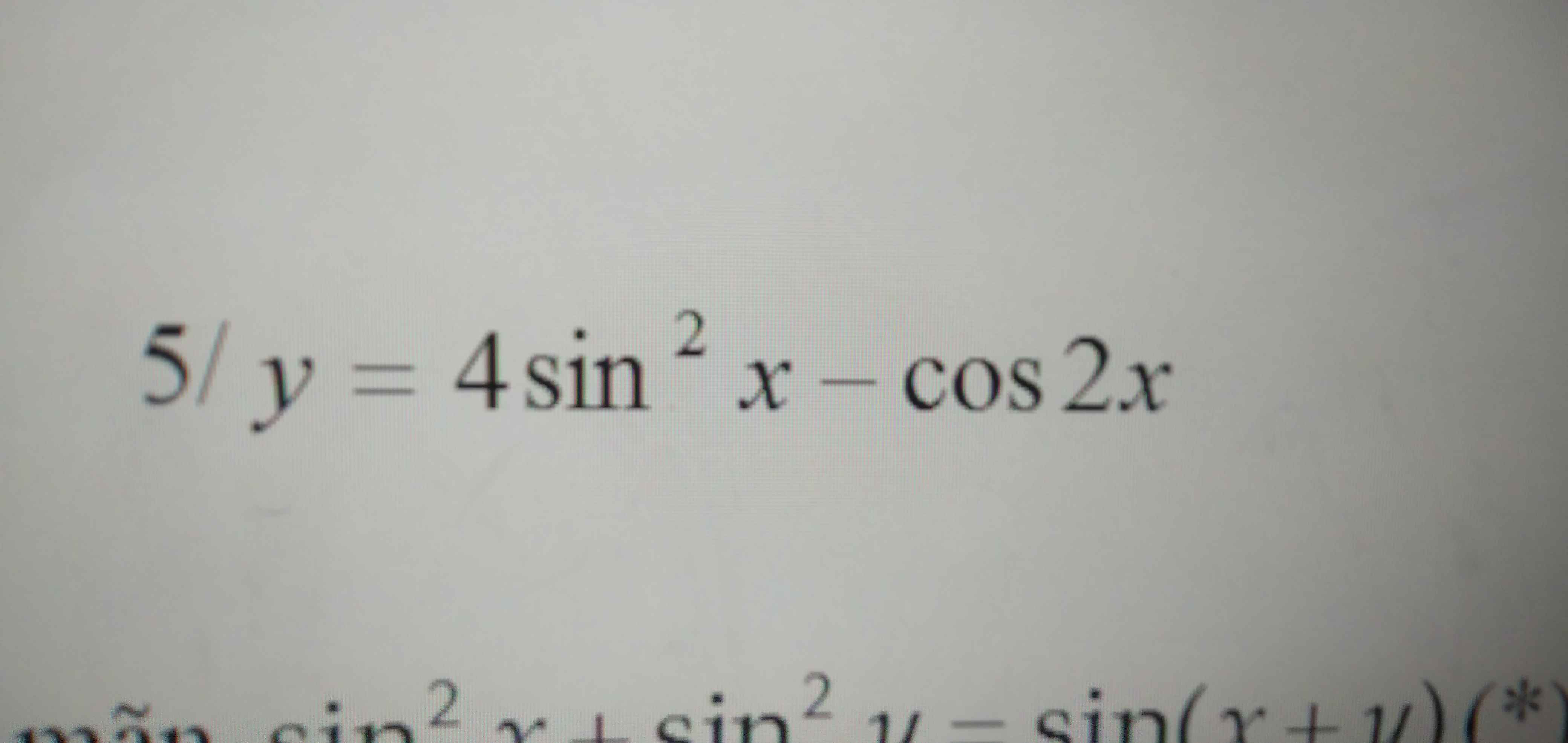
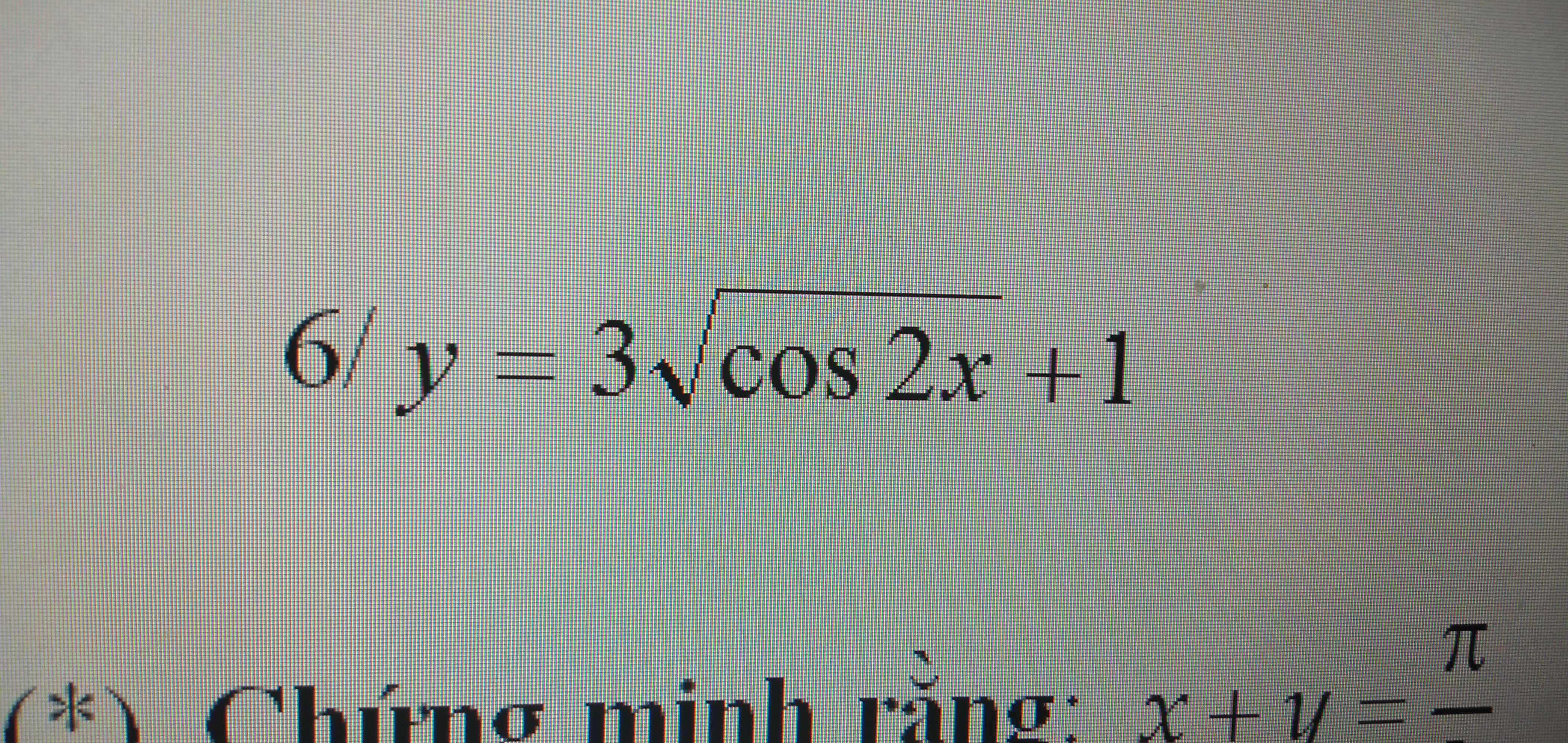
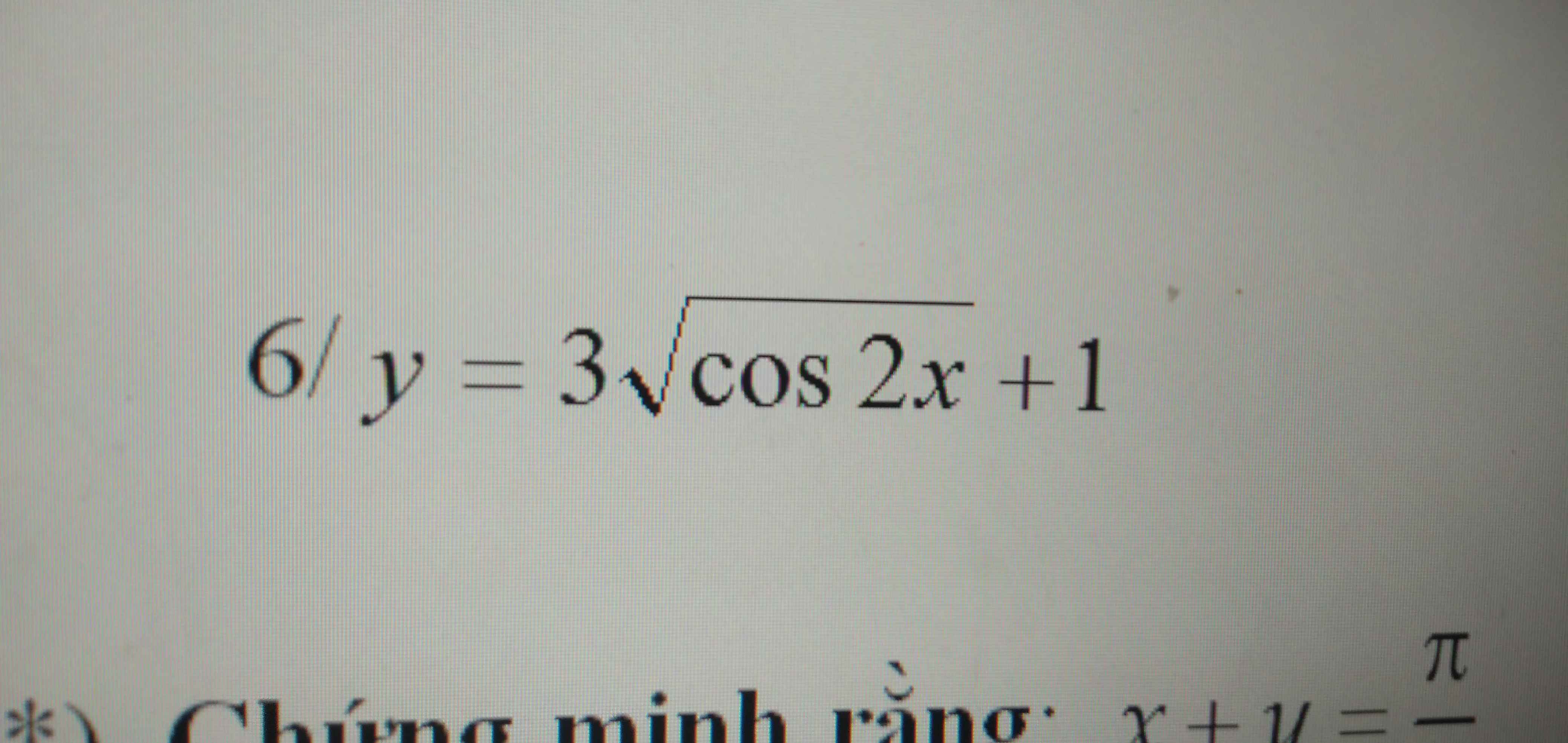
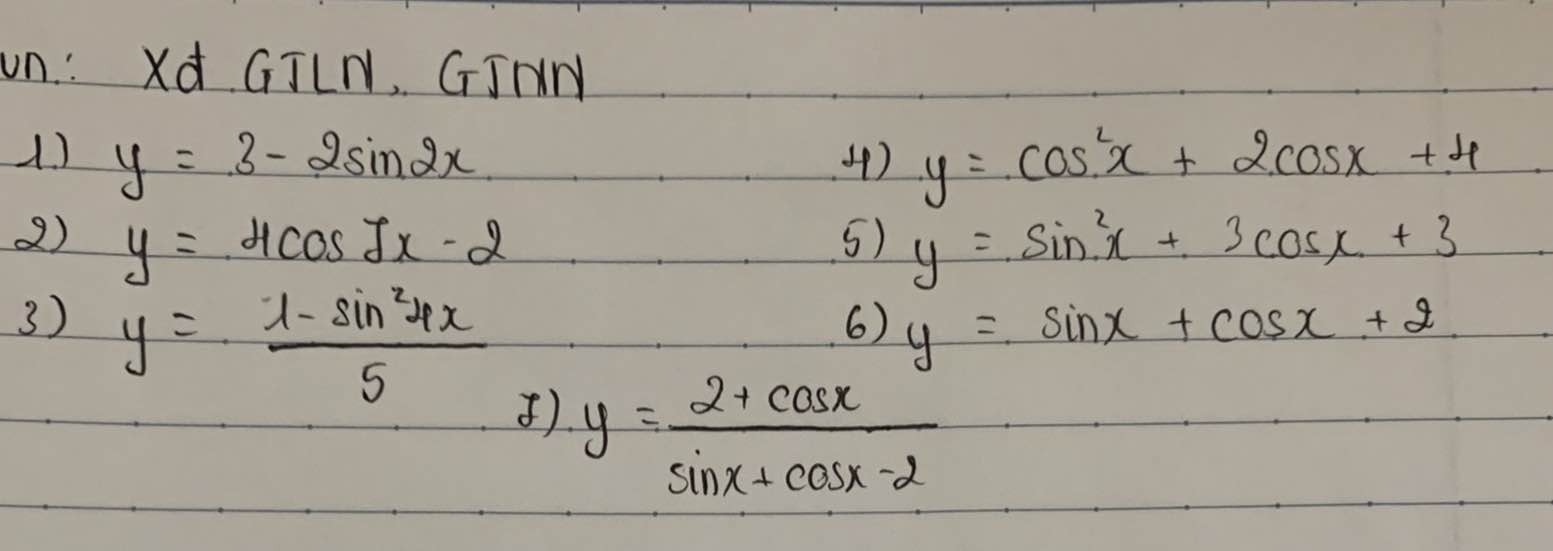
Do \(0\le cos^2x\le1\Rightarrow\dfrac{1}{2}\le y\le2\)
\(y_{min}=\dfrac{1}{2}\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
\(y_{max}=2\) khi \(cos^2x=1\Rightarrow sinx=0\Rightarrow x=k\pi\)