Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

| xy | \(6x^2y\) | \(5x^2y\) |
| xy | \(12x^3y^2\) | \(15x^3y^2\) |
| xy | \(2x^2y\) | \(-x^2y\) |
| xy | \(xy^3\) | \(\dfrac{-1}{2}xy^3\) |

Theo đề bài, x và y là hai đại lượng tỉ lệ thuận nên y = kx
Mà khi x =-1 thì y = 2 nên 2 = k.(-1) ⇒⇒ k = -2
Ta điền vào bảng sau:
|
x |
-2 |
-1 |
1 |
3 |
4 |
|
y |
4 |
2 |
-2 |
-6 |
-8 |
x và y tỉ lệ thuận nên y = k.x
Từ đó ta tìm được y lần lượt là:
(-2).(-3) = 6 ; (-2) (-1) = 2;
(-2).1 = (-2) ; (-2).5 = -10
Ta được bảng sau
| x | -3 | -1 | 1 | 2 | 5 |
| y | 6 | 2 | -2 | -4 | -10 |

Câu 2:
a. \(2xy^2+\left(-6xy^2\right)+3xy^2\)
\(=\left(2-6+3\right)xy^2\)
\(=-1xy^2\)
b. \(12x^2yz.\left(-\dfrac{3}{4}x^3y^2\right)\)
\(=12.\left(-\dfrac{3}{4}\right).x^2yz.x^3y^2\)
\(=-9x^5y^3z\)
Câu 3:
a. \(P\left(x\right)=5x^3-3x+7-x\)
\(=\left(-3x-x\right)+5x^3+7\)
\(=-4x+5x^3+7\)
\(Q\left(x\right)=-5x^3+2x-3+2x-x^2-2\)
\(=\left(2x+2x\right)+\left(-3-2\right)-5x^3-x^2\)
\(=4x+\left(-5\right)-5x^3-x^2\)
b. \(P\left(x\right)+Q\left(x\right)=\left(-4x+5x^3+7\right)+\left(4x-5-5x^3-x^2\right)\)
\(=-4x+5x^3+7+4x-5-5x^3-x^2\)
\(=\left(-4x+4x\right)+\left(5x^3-5x^3\right)+\left(7-5\right)+x^2\)
\(=2+x^2\)
Tick nha!![]()

1) a) Dấu hiệu là: thời gian giải 1 bài toán của hs lp 7C
Số các giá trị là: 36
b)c) pn tự lm nka,
3)a) \(^{3^6}\)
b) \(5^3\)
c) \(10x^5y^5\)
d) \(2x\)
Bn tự bẻ hình nha:
Câu 4:
a) Xét ΔABIvà ΔACI có:
AB = AC (\(\Delta ABC\) cân tại A)
\(\widehat{BAI}=\widehat{CAI}\) (AI là đường phân giác của \(\Delta ABC\))
AI là cạnh chung
Vậy ΔABI = ΔACI (c.g.c)
b) Vì AI là đường phân giác của \(\Delta ABC\) cân tại A nên AI đồng thời là đường trung tuyến của \(\Delta ABC\).
c) Vì AI là đường trung tuyến của \(\Delta ABC\) nên
AG = \(\dfrac{2}{3}\) AI = \(\dfrac{2}{3}\) . 9 = 6 (cm)
Câu d) mk k biết làm
Mk k chắc nên có j sai thì bn ns vs mk nha! Đúng thì tick giúp mk nhé! Chúc bn học tốt!![]()

Câu 7:
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
hay ΔDFC cân tại D
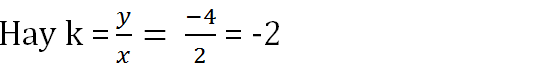
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
b: BH=CH=BC/2=3(cm)
nên AH=4(cm)