

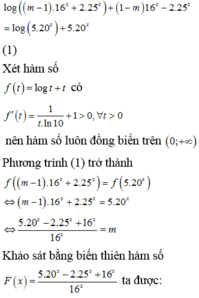
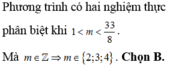
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


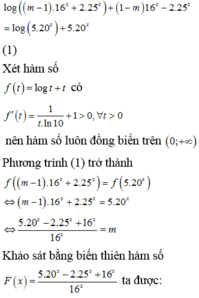
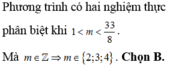


\(f'\left(x\right)=m^2x^4-mx^2+20x-\left(m^2-m-20\right)\)
Để hàm số đồng biến trên \(ℝ\)thì \(f'\left(x\right)\ge0,\)với mọi \(x\inℝ\).
Mà ta thấy \(f'\left(-1\right)=m^2-m-20-\left(m^2-m-20\right)=0\)
do đó \(x=-1\)là một điểm cực trị của hàm số \(f'\left(x\right)\).
Ta có: \(f''\left(x\right)=4m^2x^3-2mx+20\)
\(f''\left(-1\right)=0\Leftrightarrow-4m^2+2m+20=0\Leftrightarrow\orbr{\begin{cases}m=\frac{5}{2}\\m=-2\end{cases}}\).
Thử lại.
Với \(m=\frac{5}{2}\): \(f''\left(x\right)=25x^3-5x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\)
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Với \(m=-2\): \(f''\left(x\right)=16x^3+4x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\).
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Vậy tổng các giá trị của \(m\)là: \(\frac{5}{2}+\left(-2\right)=\frac{1}{2}\).
Chọn D.

Đáp án A
+)![]() (
(![]() )
)
Điều kiện:![]()
+)![]()
Đặt:![]()
![]()
![]()
![]()
![]()
Đặt![]()
![]() .
.![]()
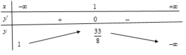
Bảng biến thiên
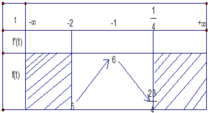
+) ![]()
Để phương trình có hai nghiệm phân biệt![]()
Do đó để phương trình có hai nghiệm phân biệt thì phương trình![]() có nghiệm
có nghiệm![]()
Từ bảng biến thiên![]() .
.

ĐKXĐ: \(mx-5>0\) ; \(x>-2\)
\(log_{mx-5}\left(x^2-6x+12\right)=log_{mx-5}\left(x+2\right)\)
\(\Rightarrow x^2-6x+12=x+2\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
TH1: \(x=2\) là nghiệm duy nhất \(\Rightarrow\left\{{}\begin{matrix}m.2-5>0\\m.5-5< 0\end{matrix}\right.\) \(\Rightarrow\) ktm
TH2: \(x=5\) là nghiệm duy nhất \(\Rightarrow\left\{{}\begin{matrix}m.2-5< 0\\m.5-5>0\end{matrix}\right.\)
\(\Rightarrow1< m< \dfrac{5}{2}\Rightarrow m=2\)

\(f\left(x\right)=x^4-6mx^2+m^2\Rightarrow f'\left(x\right)=4x^3-12mx\)
\(f'\left(x\right)=0\Leftrightarrow4x\left(x^2-3m\right)=0\)
- Nếu \(m\le0\Rightarrow\) hàm đạt GTLN tại \(x=-2\)
\(f\left(-2\right)=m^2-24m+16=16\Rightarrow\left[{}\begin{matrix}m=0\\m=24\left(ktm\right)\end{matrix}\right.\)
- Nếu \(m>0\) hàm có 3 cực trị: \(x=0\) là cực đại, \(x=\pm\sqrt{3m}\) là 1 cực tiểu
TH1: \(m\ge\frac{4}{3}\Rightarrow-\sqrt{3m}\le-2< 1< \sqrt{3m}\)
\(\Rightarrow f\left(x\right)_{max}=f\left(0\right)=m^2=16\Rightarrow m=4\) (thỏa mãn)
- Nếu \(0< m< \frac{4}{3}\)
\(\Rightarrow f\left(x\right)_{max}=max\left\{f\left(0\right);f\left(-2\right)\right\}=max\left\{m^2;m^2-24m+16\right\}\)
+ Với \(m< \frac{2}{3}\Rightarrow f\left(x\right)_{max}=f\left(-2\right)=m^2-24m+16=16\)
\(\Rightarrow\left[{}\begin{matrix}m=0\\m=24\end{matrix}\right.\) (ktm)
- Với \(\frac{2}{3}\le m< \frac{4}{3}\Rightarrow f\left(x\right)_{max}=f\left(0\right)=m^2< \frac{16}{9}< 16\left(ktm\right)\)
Vậy \(S=\left\{0;4\right\}\)
Cho e hỏi đoạn nếu 0<m<4/3 sao suy ra được f max chỉ có thể là f(0) hoặc f(-2) ạ? Còn f(1) thì sao ạ? Em cảm ơn ạ

Đáp án B

Phương trình (1) có hai nghiệm dương phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt lớn hơn 1.
Bảng biến thiên của hàm số y = t 2 - 10 t
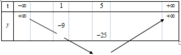
Phương trình (2) có hai nghiệm phân biệt lớn hơn 1 khi và chỉ khi -25< m < -9
Vậy S = {-24;-23;...;-10} và n(S) =15