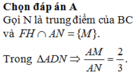Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

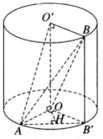
Vì trục OO’ vuông góc với các đáy nên OO′ ⊥ OA; OO′ ⊥ O′B. Vậy các tam giác AOO’ và BO’O vuông tại O và O’.
Theo giả thiết ta có AO ⊥ O′B mà AO ⊥ OO′ ⇒ AO ⊥ (OO′B). Do đó, AO ⊥ OB nên tam giác AOB vuông tại O. Tương tự, ta chứng minh được tam giác AO’B vuông tại O’. Thể tích hình chóp OABO’ là:
![]()
Hay
![]()

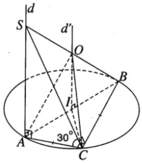
Gọi I là trung điểm của cạnh AB. Vì tam giác ABC vuông cân tại C nên ta có IA = IB = IC. Vậy I là tâm đường tròn ngoại tiếp tam giác ABC. Do đó, tâm mặt cầu ngoại tiếp tứ diện SABC phải nằm trên đường thẳng d’ vuông góc với mặt phẳng (ABC) tại I. Ta suy ra d’ // d. Do đó d’ cắt SB tại trung điểm O của đoạn SB. Ta có OB = OS = OA = OC và như vậy O là tâm đường tròn ngoại tiếp tứ diện SABC.


Vậy \(SB^2=\dfrac{6a^2}{9}+4a^2=\dfrac{42a^2}{9}\)
Do đó \(SB=\dfrac{a\sqrt{42}}{3}\)
Ta suy ra :
\(r=\dfrac{SB}{2}=\dfrac{a\sqrt{42}}{6}\)

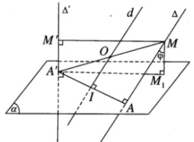
Theo giả thiết ta có: ∠A′M′M = ∠A′AM = ∠A′M1M = 90o
Do đó 5 điểm A, A’, M, M’, M1 cùng thuộc mặt cầu (S) tâm O, với O là trung điểm của A’M và có bán kính r = A′M2
Mặt khác ta có A’M2 = A’A2 + AM2
Trong đó
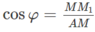
Do đó
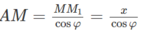
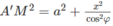
Mặt cầu tâm O có bán kính
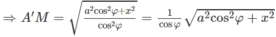
Diện tích của mặt cầu tâm O là:
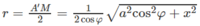

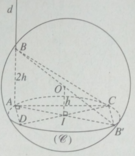
Diện tích tam giác BCD bằng:
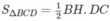
Diện tích này lớn nhất khi AI // CD.