Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Pt hoành độ giao điểm của đồ thị hàm số (C) với đường thẳng d là:
\(\dfrac{x-1}{x+1}=m-x\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\g\left(x\right)=x^2+\left(2-m\right)x-m-1=0\left(1\right)\end{matrix}\right.\)
Đồ thị (C) cắt đường thẳng d tại 2 điểm phân biệt <=> pt(1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\g\left(-1\right)\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2+8>0\\-2\ne0\end{matrix}\right.\)
Khi đó: \(x_A,x_B\) là nghiệm của pt (1). Vì tiếp tuyến tại A và B //
\(\Rightarrow f'\left(x_A\right)=f'\left(x_B\right)\Leftrightarrow\dfrac{2}{\left(x_A+1\right)^2}=\dfrac{2}{\left(x_B+1\right)^2}\Leftrightarrow\left[{}\begin{matrix}x_A=x_B\left(loai\right)\\x_A+x_B=-2\end{matrix}\right.\)
Theo định lí Viet ta có:
\(x_A+x_B=m-2\Rightarrow m-2=-2\Leftrightarrow m=0\)
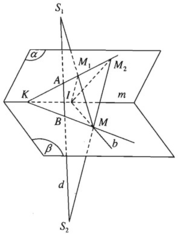
a) Mặt phẳng (M, d) cắt (α) theo giao tuyến M 1 M 2 . Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M 1 M 2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt (β) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng ( S 1 , b ) luôn luôn cắt (α) theo giao tuyến I M 1 . Do đó điểm M 1 di động trên giao tuyến của I M 1 cố định. Còn khi M di động trên b thì mặt phẳng ( S 2 , b ) cắt (α) theo giao tuyến I M 2 . Do đó điểm M 2 chạy trên giao tuyến I M 2 cố định.
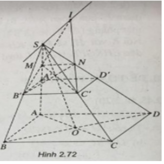
a) (P) // BC nên (P) sẽ cắt (SBC) theo giao tuyến B'C' song song với BC.
Tương tự, (P) cắt (SAD) theo giao tuyến MN song song với AD.
Khi M trùng với trung điểm A' của cạnh SA thì thiết diện MB'C'N' là hình bình hành.
b) Với M không trùng với A':
Gọi I ∈ B′M ∩ C′N. Ta có:
I ∈ B′M ⊂ (SAB), tương tự I′ ∈ C′N ⊂ (SCD)
Như vậy I ∈ Δ = (SAB) ∩ (SCD).
Gọi điểm cố định có tọa độ \(x_0;y_0\Rightarrow\) với mọi M ta có:
\(x_0^4-y_0+1-m\left(x_0^2-4\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0^2-4=0\\x_0^4-y_0+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A\left(2;17\right)\\B\left(-2;17\right)\end{matrix}\right.\)
\(y'=4x^3-2mx\) \(\Rightarrow\left\{{}\begin{matrix}y'\left(2\right)=32-4m\\y'\left(-2\right)=-32+4m\end{matrix}\right.\)
Tiếp tuyến tại A: \(y=\left(32-4m\right)\left(x-2\right)+17=\left(32-4m\right)x+8m-47\)
Tiếp tuyến tại B: \(y=\left(4m-32\right)\left(x+2\right)+17=\left(4m-32\right)x+8m-47\)
Hai tiếp tuyến song song khi: \(\left\{{}\begin{matrix}32-4m=4m-32\\8m-17\ne8m-17\end{matrix}\right.\)
Không tồn tại m thỏa mãn
Vì phương trình tiếp tuyến song song với đường thẳngy =-3x + 1nên nó có hệ số góc là -3
Do đó f ' x = 3 x 2 − 10 x = − 3 ⇔ 3 x 2 − 10 x + 3 = 0
⇔ x = 1 3 x = 3
Với x = 1 3 thì y 0 = 40 27 Vậy phương trình tiếp tuyến là: y = − 3 x − 1 3 + 40 27 = − 3 x + 67 27
Với x=3thì y 0 = - 16 Vậy phương trình tiếp tuyến là: y = -3(x- 3) – 16 = - 3x – 7
Chọn đáp án C
Chọn A.
Ta có: y’ = 3x2 – 4x + 2.
Tiếp tuyến tại M, N của (C) vuông góc với đường thẳng y = -x + 2017. Nên tiếp tuyến tại M và N có hệ số góc là 1
Hoành độ x1, x2 của các điểm M, N là nghiệm của phương trình 3x2 – 4x + 2 = 1.
Suy ra x1 + x2 = 4/3 ( hệ thức Vi-et).
Gọi tọa độ điểm MM, NN lần lượt là M(x1;y1), N(x2;y2)M(x1;y1), N(x2;y2).
Hệ số góc tiếp tuyến của (C)(C) tại MM và NN lần lượt là
k1=y′(x1)=−3x12+6x1−1k1=y′(x1)=−3x12+6x1−1; k2=y′(x2)=−3x22+6x2−1k2=y′(x2)=−3x22+6x2−1
Để tiếp tuyến của (C)(C) tại MM và NN luôn song song với nhau điều kiện là
{k1=k2x1≠x2{k1=k2x1≠x2 ⇔{(x1−x2)[−3(x1+x2)+6]=0x1≠x2⇔{(x1−x2)[−3(x1+x2)+6]=0x1≠x2⇔x1+x2=2⇔x1+x2=2.
Ta có:y1+y2=−(x1+x2)[(x1+x2)2−3x1x2]+3[(x1+x2)2−2x1x2]−(x1+x2)+8y1+y2=−(x1+x2)[(x1+x2)2−3x1x2]+3[(x1+x2)2−2x1x2]−(x1+x2)+8
Do x1+x2=2x1+x2=2 nên y1+y2=−2(4−3x1x2)+3(4−2x1x2)+8=10y1+y2=−2(4−3x1x2)+3(4−2x1x2)+8=10.
Trung điểm của đoạn MNMN là I(1;5)I(1;5). Vậy đường thẳng MNMN luôn đi qua điểm cố định I(1;5)I(1;5).
Ta có \(y'=-3x^2+6x-1\Rightarrow y^n=-6x+6;y^n=0\Leftrightarrow x=1\Rightarrow I\left(1;5\right)\) là điểm uốn của đồ thị (C)
G/s M (xM;yM); N(xN;yN) là 2 điểm di động trên (C)
Tiếp tuyển của (C) tại M,N song song với nhau
=> y'(xM)=y'(xN)
\(\Leftrightarrow-3x^2_M+6x_M-1=-3x_N^2+6x_N-1\)
\(\Leftrightarrow-3\left(x_M-x_N\right)\left(x_N+x_M\right)+6\left(x_M-x_N\right)=0\)
\(\Leftrightarrow\frac{x_M+x_N}{2}=1\left(x_M\ne x_N\right)\)=> I là trung điểm MN
Vậy đường thẳng MN luôn đi qua điểm I cố định