Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: D
a sai vì nếu tam giác ABC thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC vuông tại A không phải vuông tại B.
b, c, d đúng.

Đáp án :
B. Đồ thị hàm số chẵn nhận trục hoành làm trục đối xứng.

+) Mô tả tập hợp D = {các hình vuông}
+) Mô tả tập hợp C = {các hình bình hành có hai đường chéo vuông góc} = {Các hình thoi}.
Thật vậy,
Xét tứ giác ABCD, là hình hình hành có hai đường chéo vuông góc.
Gọi \(AC \cap BD = O\) thì O là trung điểm của AC và BD.
Ta có: AO vừa là trung tuyến vừa là đường cao.
\( \Rightarrow \Delta ABD\) cân tại A.
\( \Rightarrow AB = AD\).
Tương tự ta cũng có: \(CB = CD\).
Mà \(AB = CD;\;AD = BC\).
Do đó: \(AB = CD = \;AD = BC\) hay tứ giác ABCD là hình thoi.
a) Vì nhiều hình thoi (các hình thoi không có góc nào vuông) thì không phải là hình vuông, nên \(C\not{ \subset }D\).
Vậy mệnh đề “\(C \subset D\)” sai.
b) Vì mỗi hình vuông cũng là một hình thoi (hình thoi đặc biệt: có một góc vuông), nên các phần tử của D cũng là phần tử của C. Hay \(C \supset D\)
Do đó mệnh đề “\(C \supset D\)” đúng.
c) Vì \(\left\{ \begin{array}{l}C \subset D\\C \supset D\end{array} \right.\;\; \Rightarrow C \ne D\)
Vậy mệnh đề “\(C = D\)” sai.

a) “\(\forall x \in \mathbb{R},x + ( - x) = 0\)”
b) “\(\exists n \in \mathbb{N},{x^2} = 9\)”

Đáp án: C
Hình vuông là hình thoi đặc biệt có 4 góc vuông nên V ⊂ T đúng.
Hình vuông là hình chữ nhật đặc biệt có 4 cạnh bằng nhau nên V ⊂ N đúng.
Hình thoi là hình bình hành đặc biệt có 4 cạnh bằng nhau nên H ⊂ T sai.
Hình chữ nhật là hình bình hành đặc biệt có 4 góc vuông nên N ⊂ H đúng.

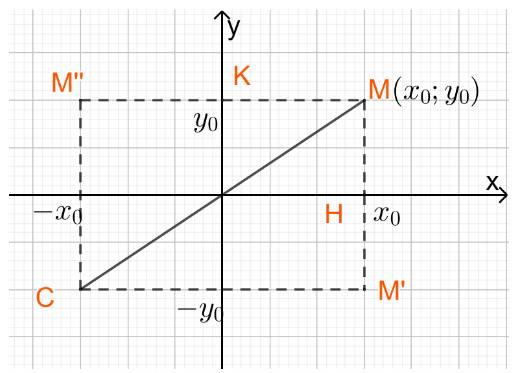
a) H là hình chiếu vuông góc của M trên trục Ox nên tọa độ điểm H là \(H\left( {{x_0};0} \right)\)
b) M’ đối xứng với M qua trục Ox nên H là trung điểm của MM’
Suy ra \({x_{M'}} = 2{x_H} - {x_M} = 2{x_0} - {x_0} = {x_0};{y_{M'}} = 2{y_H} - {y_M} = 2.0 - {y_0} = - {y_0}\)
Vậy tọa độ điểm M’ là \(\left( {{x_0}; - {y_0}} \right)\)
c) K là hình chiếu vuông góc của M trên trục Oy nên tọa độ điểm K là \(K\left( {0;{y_0}} \right)\)
d) M’’ đối xứng với M qua trục Oy nên K là trung điểm của MM’’
Suy ra \({x_{M''}} = 2{x_K} - {x_M} = 2.0 - {x_0} = - {x_0};{y_{M''}} = 2{y_K} - {y_M} = 2{y_0} - {y_0} = {y_0}\)
Vậy tọa độ điểm M'' là \(\left( { - {x_0};{y_0}} \right)\)
e) C đối xứng với M qua gốc tọa độ nên O là trung điểm của MC
Suy ra \({x_C} = 2{x_O} - {x_M} = 2.0 - {x_0} = - {x_0};{y_C} = 2{y_O} - {y_M} = 2.0 - {y_0} = - {y_0}\)
Vậy tọa độ điểm C là \(\left( { - {x_0}; - {y_0}} \right)\)

a) Mệnh đề P đúng, vì: \(\left| x \right| = \left\{ \begin{array}{l}x\quad \;\;(x \ge 0)\\ - x\quad (x < 0)\end{array} \right.\) nên \(\left| x \right| \ge x\).
Mệnh đề Q sai vì chỉ có các số \( \pm \sqrt {10} \) có bình phương bằng 10, nhưng \(\sqrt {10} \) và \( - \sqrt {10} \) đều không là số tự nhiên.
Mệnh đề R đúng vì \(x = - 1 + \sqrt 2 \in \mathbb{R}\) thỏa mãn \({x^2} + 2x - 1 = 0.\)
b) Có thể viết lại các mệnh đề trên như sau:
P: “\(\forall x \in \mathbb{R},\;\left| x \right| \ge x\)”
Q: “\(\exists n \in \mathbb{N},{n^2} = 10\)”
R: “\(\exists x \in \mathbb{R},\;{x^2} + 2x - 1 = 0\)”

\(d\left(A\left(P\right)\right)=\frac{\left|2\left(-2\right)-2.1+1.5-1\right|}{\sqrt{2^2+\left(-2\right)^2+1^2}}=\frac{2}{3}\)
(P) có vectơ pháp tuyến là \(\overrightarrow{n_p}=\left(2;-2;1\right);\)
d có vectơ pháp tuyến là \(\overrightarrow{u_d}=\left(2;3;1\right);\left[\overrightarrow{n_p},\overrightarrow{u_d}\right]=\left(-5;0;10\right)\)
Theo giả thiết suy ra (Q) nhận \(\overrightarrow{n}=-\frac{1}{5}\left[\overrightarrow{n_p},\overrightarrow{u_d}\right]=\left(1;0;-2\right)\) làm vectơ pháp tuyến
Suy ra \(\left(Q\right):x-2z+12=0\)

a) An: "\(\forall x \in \mathbb R ,{x^2} \ge 0\)"
b) Bình: "\(\exists x \in ,{x^2} < 0\)"