Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C
I.Sai ví dụ hàm số y = x 3 đồng biến trên
(−¥; +¥) nhưng y' ³ 0, "x Î (−¥; +¥)
II.Đúng
III.Đúng

Đáp án D
Định lí: “Nếu hàm số y = f x liên tục trên a ; b và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho f c = 0 ”.
Mệnh đề 1: SAI ở giả thiết (a;b).
Mệnh đề 2: Nếu hàm số y=f(x) liên tục trên a ; b
và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho c hay f x = 0 là nghiệm của phương trình f(x)=0 nên mệnh đề 2 ĐÚNG.
Mệnh đề 3: Nếu hàm số y=f(x) liên tục, đơn điệu trên a ; b và f a . f b < 0 thì đồ thị hàm số y=f(x) cắt trục Ox tại duy nhất một điểm thuộc khoảng (a;b) nên f(x)=0 có nghiệm duy nhất trên (a;b). Do đó mệnh đề 3 ĐÚNG

Đáp án B.
Phương pháp : Chuyển vế, lấy nguyên hàm hai vế.
Cách giải :
![]()
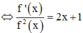
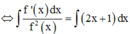
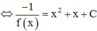
![]()
![]()
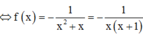
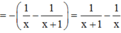
![]()
![]()
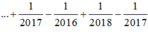
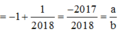
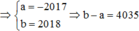

Đáp án B
Do f 0 < 0 < f − 1 nên phương trình f x = 0 có ít nhất 1 nghiệm x ∈ − 1 ; 0
Đáp án đúng là S = ∫ − 1 1 f x d x
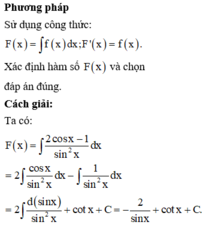
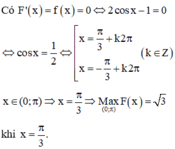
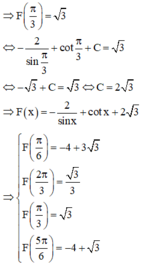



Chọn A.
Phương pháp:
Sử dụng phương pháp nguyên hàm từng phần hai lần để tìm F(x )
Cách giải: