Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

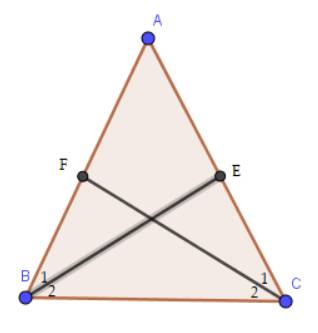
Vì tam giác ABC cân tại A nên AB = AC; \(\widehat {ABC} = \widehat {ACB}\) ( tính chất)
Vì BE là là tia phân giác của góc ABC nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)
Vì CF là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)
Do đó, \(\widehat {{B_1}} = \widehat {{C_1}}\)
Xét \(\Delta ABE\) và \(\Delta ACF\), ta có:
\(\widehat A\) chung
AB = AC
\(\widehat {{B_1}} = \widehat {{C_1}}\)
\( \Rightarrow \Delta ABE = \Delta ACF\left( {g.c.g} \right)\)
\( \Rightarrow \)BE = CF ( 2 cạnh tương ứng)

JUNPHAM2018 đúng rồi !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

a: Xét ΔAEB và ΔAFC có
\(\widehat{ABE}=\widehat{ACF}\)
AB=AC
\(\widehat{BAC}\) chung
Do đó: ΔAEB=ΔAFC
Suy ra: AE=AF
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
c: Xét ΔFBI và ΔECI có
\(\widehat{FBI}=\widehat{ECI}\)
FB=EC
\(\widehat{BFI}=\widehat{CEI}\)
Do đó: ΔFBI=ΔECI
Suy ra: IB=IC
hay I nằm trên đường trung trực của BC(1)
Ta có: AB=AC
nên A nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AI\(\perp\)BC
d: Xét ΔBIC có IB=IC
nên ΔBIC cân tại I

B A C E F O
a/ Giải thích thêm: Vì AB = AC (tam giác ABC cân tại A. Mà E là trung điểm AC;F là trung điểm AB => AF = BF = AE = EC)
Xét tam giác BAE và tam giác CAF có:
\(\hept{\begin{cases}\widehat{BAC}:chung\\AB=AC\left(gt\right)\\AE=AF\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta BAE=\Delta CAF\left(c.g.c\right)\)
\(\Rightarrow BE=CF\)
b/ Xét tam giác ABC có 2 đường trung tuyến BE;CF cắt nhau tại O
=> O là trọng tâm tam giác ABC
=> AO là đường trung tuyến thứ 3
=> AO đi qua trung điểm H của BC (Bạn bổ sung điểm H cho mình nhá - Cho dễ làm thôi)
Mà tam giác ABC cân tại A => AO vừa là đường trung tuyến vừa là đường cao
\(\Rightarrow AO⊥BC\)tại H
c/ Vì H là trung điểm BC => HB = HC = BC:2 = 10 : 2 = 5 (cm)
Xét tam giác ABH vuông tại H có:
\(AH^2+BH^2=AB^2\left(pytago\right)\)
\(AH^2+5^2=13^2\)
\(\Rightarrow AH^2=13^2-5^2=169-25=144\)
\(\Rightarrow AH=\sqrt{144}=12\left(cm\right)\)
Vì O là trọng tâm của tam giác ABC => \(OH=\frac{1}{3}AH\Rightarrow OH=\frac{1}{3}.12=4\left(cm\right)\)
Xét tam giác BOH vuông tại H có:
\(BH^2+OH^2=BO^2\left(pytago\right)\)
\(5^2+4^2=BO^2\)
\(25+16=BO^2\)
\(41=BO^2\)
\(\Rightarrow BO=\sqrt{41}\approx6,4\left(cm\right)\)

a) Tam giác ABE ( góc E=90 độ) và Tam giác ACF ( góc F=90 độ), có:
AB = AC ( gt )
Góc A chung
=> tam giác ... = tam giac ... ( cạnh huyền - góc nhọn)
=> BE = CF và góc ABE = góc ACF
b) Tam giác FCB ( góc F = 90 độ) và tam giác BEC ( góc E=90 độ), có:
BC chung
FC = EB ( c/m trên)
=> tam giác... = tam giác... ( cạnh huyền-cạnh góc vuông)
=> FB=EC
Tam giác ECI và tam giác FBI, có:
EC=FB (c/m trên)
góc E= góc F (=90 độ)
góc ACF = góc ABE (c/m trên)
=> tam giác ...= tam giác... (g-c-g)
c) Ta có: FA=AB - FB
EA=AC - EC
mà AB=AC; FB=EC
=> FA=EA
tam giác AIF(F=90 độ) tam giác AIE (E = 90 độ), có:
AI chung
FA=EA (c/ m trên)
=> tam giác... = tam giác... ( cạnh huyền-cạnh góc vuông)
=> góc BAI = góc CAI
hay AI là phân giác của góc A
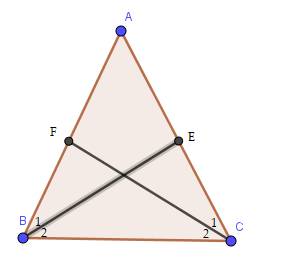
Ta có: \(\widehat{ABE}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACF}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABE}=\widehat{ACF}\)
Xét ΔABE và ΔACF có
\(\widehat{ABE}=\widehat{ACF}\)
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
=>BE=CF