Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
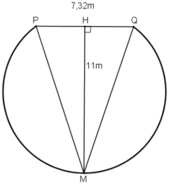
Gọi vị trí đặt quả bóng để sút phạt đền là M, và bề ngang cầu môn là PQ thì M nằm trên đường trung trực của PQ.
Gọi H là trung điểm của PQ, ta có:
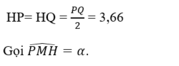
Do M nằm trên đường trung trực của PQ nên MH vuông góc PQ.
Tam giác MPH vuông tại H, áp dụng tỉ số lượng giác trong tam giác vuông ta có:
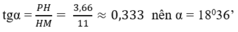
Vậy góc sút phạt đền là 2α ≈ 37012’
+ Vẽ cung chứa góc 37012’ dựng trên đoạn thẳng PQ. Bất cứ điểm nào trên cung vừa vẽ cũng có cùng “góc sút” như quả phạt đền 11m.
Kiến thức áp dụng
+ Trong một tam giác vuông, tan α = cạnh đối / cạnh huyền.
Gọi vị trí đặt bóng để sút phạt đền là M, và bề ngang cầu môn là PQ thì M nằm trên đường trung trực của PQ. Gọi H là trung điểm PQ, \(\widehat{PMH}=\alpha\)
Theo các giả thiết đã cho thì trong tam giác vuông MHP, ta có:
tg\(\alpha\) = \(\dfrac{3,66}{11}\approx\) 0,333 => \(\alpha\)= 18o36’.
Vậy góc sút phạt đền là 2α \(\approx\)37o12'
Hướng dẫn giải:
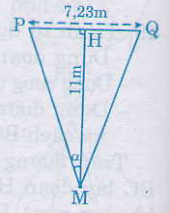
Gọi vị trí đặt bóng để sút phạt đền là M, và bề ngang cầu môn là PQ thì M nằm trên đường trung trực của PQ. Gọi H là trung điểm PQ, = α.
Theo các giả thiết đã cho thì trong tam giác vuông MHP, ta có:
tgα = ≈ 0,333 => α = 18o36’.
Vậy góc sút phạt đền là 2α ≈ 37o12’
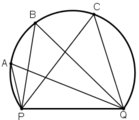
Các điểm A, B, C, Q, P cùng thuộc một đường tròn.
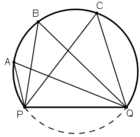
Các góc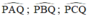 
đều là các góc nội tiếp cùng chắn cung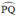 
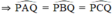
Kiến thức áp dụng
+ Trong cùng một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
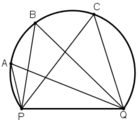
Các điểm A, B, C, Q, P cùng thuộc một đường tròn.
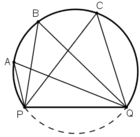
Các góc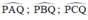 
đều là các góc nội tiếp cùng chắn cung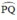 
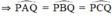
- Áp dụng tỉ số lượng giác vào tam giác ABC vuông tại B
\(\Rightarrow tan60=\dfrac{h}{BC}\)
\(\Rightarrow BC=\dfrac{h\sqrt{3}}{3}\)
\(\Rightarrow BD=BC+CD=\dfrac{h\sqrt{3}}{3}+600\)
- Áp dụng tỉ số lượng giác vào tam giác ABD vuông tại B
\(tan50=\dfrac{h}{BD}\)
\(\Rightarrow h=tan50.\left(\dfrac{h\sqrt{3}}{3}+600\right)\)
\(\Rightarrow h\approx2292m\)
Vậy ...
Gọi vị trí đặt quả bóng để sút phạt đền là M, và bề ngang cầu môn là PQ thì M nằm trên đường trung trực của PQ.
Gọi H là trung điểm của PQ, ta có:
Do M nằm trên đường trung trực của PQ nên MH vuông góc PQ.
Tam giác MPH vuông tại H, áp dụng tỉ số lượng giác trong tam giác vuông ta có:
Vậy góc sút phạt đền là 2α ≈ 37012’
+ Vẽ cung chứa góc 37012’ dựng trên đoạn thẳng PQ. Bất cứ điểm nào trên cung vừa vẽ cũng có cùng “góc sút” như quả phạt đền 11m.