
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3
\(A=sin\left(x+\dfrac{\pi}{4}\right).cos\left(x-\dfrac{\pi}{4}\right)\\ =\dfrac{1}{2}\left[sin\left(x+\dfrac{\pi}{4}+x-\dfrac{\pi}{4}\right)+sin\left(x+\dfrac{\pi}{4}-x+\dfrac{\pi}{4}\right)\right]\\ =\dfrac{1}{2}\left(sin2x+sin\dfrac{\pi}{2}\right)\\ =\dfrac{1}{2}\left(-\dfrac{1}{3}+1\right)\\ =\dfrac{1}{3}\)
3:
\(A=\dfrac{\sqrt{2}}{2}\cdot\left(sinx+cosx\right)\cdot\dfrac{\sqrt{2}}{2}\cdot\left(sinx+cosx\right)\)
\(=\dfrac{1}{2}\cdot\left(sinx+cosx\right)^2\)
\(=\dfrac{1}{2}\left(1+sin2x\right)=\dfrac{1}{2}\left(1+\dfrac{-1}{3}\right)=\dfrac{1}{2}\cdot\dfrac{2}{3}=\dfrac{1}{3}\)

\(\dfrac{1+sin2x}{cos2x}=\dfrac{\left(sinx+cosx\right)^2}{\left(cos^2x-sin^2x\right)}=\dfrac{\left(cosx+sinx\right)^2}{\left(cosx-sinx\right)\left(cosx+sinx\right)}\)
\(=\dfrac{cosx+sinx}{cosx-sinx}\)(1)
\(\dfrac{1+tanx}{1-tanx}=\dfrac{1+\dfrac{sinx}{cosx}}{1-\dfrac{sinx}{cosx}}=\dfrac{sinx+cosx}{cosx}:\dfrac{cosx-sinx}{cosx}\)
\(=\dfrac{sinx+cosx}{cosx}\cdot\dfrac{cosx}{cosx-sinx}=\dfrac{sinx+cosx}{cosx-sinx}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{1+tanx}{1-tanx}=\dfrac{1+sin2x}{cos2x}\)


a: ĐKXĐ: sin x-1<>0
=>sin x<>1
=>x<>pi/2+k2pi
TXĐ: D=R\{pi/2+k2pi}
b: ĐKXĐ: sin x+1<>0
=>sinx<>-1
=>x<>-pi/2+k2pi
TXĐ: D=R\{-pi/2+k2pi}
c: ĐKXĐ: x-pi/3<>kpi
=>x<>kpi+pi/3
TXĐ: D=R\{pi/3+kpi}

a: tan 2x=tan pi/11
=>2x=pi/11+kpi
=>x=pi/22+kpi/2
b: tan(30 độ-3x)=tan 75 độ
=>30 độ-3x=75 độ+k*180 độ
=>3x=-45 độ-k*180 độ
=>x=-15 độ-k*60 độ

a: cotx=-căn 3/3
=>tan x=-căn 3
=>x=-pi/3+kpi
b: cot3x=cot pi/7
=>3x=pi/7+kpi
=>x=pi/21+kpi/3
c: cot(3x+30 độ)=cot(75 độ)
=>3x+30 độ=75 độ+k*180 độ
=>3x=45 độ+k*180 độ
=>x=15 độ+k*60 độ



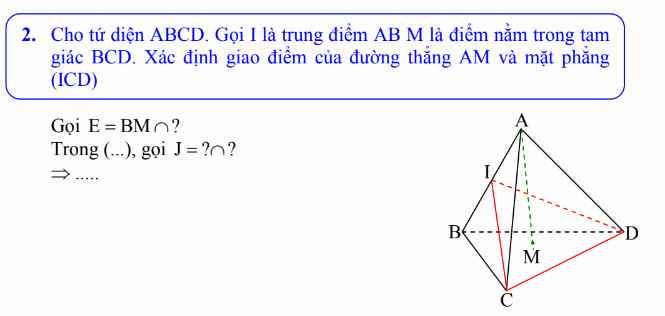 giúp vs
giúp vs giúp vs
giúp vs






a: cosx=cos15 độ
=>\(\left[{}\begin{matrix}x=15^0+k\cdot360^0\\x=-15^0+k\cdot360^0\end{matrix}\right.\)
b: \(cos2x=cos\left(x+60^0\right)\)
=>\(\left[{}\begin{matrix}2x=x+60^0+k\cdot360^0\\2x=-x-60^0+k\cdot360^0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2x-x=60^0+k\cdot360^0\\2x+x=-60^0+k\cdot360^0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=60^0+k\cdot360^0\\x=-20^0+k\cdot120^0\end{matrix}\right.\)