K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
S2
1
20 tháng 5 2022
\(\text{Δ}=\left(-3\right)^2-4\cdot\left(2m+1\right)\)
=9-8m-4=-8m+5
Để phương trình có nghiệm kép thì -8m+5=0
hay m=5/8
Pt trở thành \(x^2-3x+\dfrac{9}{4}=0\)
hay x=3/2
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
2.1
ĐKXĐ: \(x\ge-\dfrac{1}{16}\)
\(x^2-x-20-2\left(\sqrt{16x+1}-9\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4\right)-\dfrac{32\left(x-5\right)}{\sqrt{16x+1}+9}=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4-\dfrac{32}{\sqrt{16x+1}+9}\right)=0\) (1)
Do \(x\ge-\dfrac{1}{16}\Rightarrow\left\{{}\begin{matrix}\dfrac{32}{\sqrt{16x+1}+9}< \dfrac{32}{9}\\x+4\ge-\dfrac{1}{16}+4=\dfrac{63}{16}>\dfrac{32}{9}\end{matrix}\right.\)
\(\Rightarrow x+4-\dfrac{32}{\sqrt{16x+1}+9}>0\)
Nên (1) tương đương:
\(x-5=0\)
\(\Leftrightarrow x=5\)
Câu 2.2, 2.3 đề lỗi không dịch được
NH
1
31 tháng 8 2021
Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
N
1
24 tháng 6
Câu 6: Để hàm số y=(1-m)x+3 nghịch biến trên R thì 1-m<0
=>m>1
=>Chọn B
Câu 7: D
Câu 10: (D)//(D')
=>\(\left\{{}\begin{matrix}3m+1=2\left(m+1\right)\\-2\ne-2\left(loại\right)\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
=>Chọn D
Câu 11: \(x^2+2x+2=\left(x+1\right)^2+1>=1>0\forall x\)
=>\(\sqrt{x^2+2x+2}\) luôn xác định với mọi số thực x
=>Chọn A
Câu 12: Để hai đường thẳng y=x+3m+2 và y=3x+2m+3 cắt nhau tại một điểm trên trục tung thì \(\left\{{}\begin{matrix}1\ne3\left(đúng\right)\\3m+2=2m+3\end{matrix}\right.\)
=>3m+2=2m+3
=>m=1
=>Chọn C
HK
3
31 tháng 10 2021
Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi
14 tháng 5 2023
a: Thay x=0 và y=5 vào (d), ta được:
m*0+5=5
=>5=5(đúng)
=>ĐPCM
b: x1<x2; |x1|>|x2|
=>x1*x2<0
PTHĐGĐ là:
x^2-mx-5=0
Vì a*c<0
nên x1,x2 luôn trái dấu
=>Với mọi m
MA
2
PT
7 tháng 7 2019
b) \(\sqrt{25a^2}+3a\) \(=5\left|a\right|+3a\)
Vì a > 0 => |a| = a
=> 5|a| + 3a = 5a + 3a = 8a
TN
1
26 tháng 10 2021
b: \(BC=\sqrt{89}\left(cm\right)\)
\(\sin\widehat{B}=\dfrac{5\sqrt{89}}{89}\)
\(\Leftrightarrow\widehat{B}\simeq32^0\)
\(\widehat{C}=58^0\)
AH
Akai Haruma
Giáo viên
29 tháng 6 2021
1.
$(m^2-m-1)x-5m=(3-m)x$
$\Leftrightarrow (m^2-m-1+m-3)x=5m$
$\Leftrightarrow (m^2-4)x=5m$
$\Leftrightarrow (m-2)(m+2)x=5m$
Nếu $m=-2$ thì $0x=-10$ (vô lý) $\Rightarrow$ pt vô nghiệm
Nếu $m=2$ thì $0x=10$ (vô lý) $\Rightarrow$ pt vô nghiệm
Nếu $m\neq \pm 2$ thì pt có nghiệm duy nhất $x=\frac{5m}{(m-2)(m+2)}$
AH
Akai Haruma
Giáo viên
29 tháng 6 2021
2.
$m^2x+mx+x-m-2=0$
$\Leftrightarrow x(m^2+m+1)=m+2$
Vì $m^2+m+1=(m+\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}>0$ với mọi $m\in\mathbb{R}$
$\Rightarrow m^2+m+1\neq 0$
Do đó pt có nghiệm duy nhất $x=\frac{m+2}{m^2+m+1}$ với mọi $m\in\mathbb{R}$
8 tháng 12 2021
\(M=\left(\dfrac{a-1}{2\sqrt{a}}\right)^2\cdot\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\\ M=\dfrac{\left(a-1\right)^2}{4a}\cdot\dfrac{-4\sqrt{a}}{a-1}=\dfrac{1-a}{\sqrt{a}}\)
8 tháng 12 2021
anh có thể ghi thêm các bước trước khi ra đc mấy cái này ko ạ tại rút gọn quá e ch hỉu ạ e c.ơn
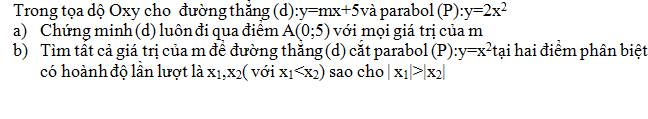
xin loi chi em moi lop 5
Bài 4 :
a, \(\sqrt{\left(4-3\sqrt{2}\right)^2}=4-3\sqrt{2}\)
b, \(\sqrt{6-2\sqrt{5}}=\sqrt{\left(\sqrt{5}-1\right)^2}=\sqrt{5}-1\)
e, \(\frac{\sqrt{2}-\sqrt{11+6\sqrt{2}}}{\sqrt{6+2\sqrt{5}}-\sqrt{5}}=\frac{\sqrt{2}+\sqrt{3^2+2.3\sqrt{2}+2}}{\sqrt{\left(\sqrt{5}+1\right)^2}-\sqrt{5}}\)
\(=\frac{\sqrt{2}+3+\sqrt{2}}{\sqrt{5}+1-\sqrt{5}}=3+2\sqrt{2}\)
h, \(\sqrt{6+2\sqrt{4-2\sqrt{3}}}=\sqrt{6+2\sqrt{\left(\sqrt{3}-1\right)^2}}\)
\(=\sqrt{6+2\left(\sqrt{3}-1\right)}=\sqrt{4+2\sqrt{3}}=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)