giúp với mng ><
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
J
3
Y
28 tháng 6 2023
\(a,A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(=x-0,2-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(=\left(-0,2-2+2\right)+\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)\)
\(=-0,2\)
\(b,B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(=x^3-8y^3-x^3+8y^3-10\)
\(=-10\)
\(c,C=4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x-1\right)\left(x+1\right)-4x\)
\(=4\left(x^2+2x+1\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=13\)
H9
HT.Phong (9A5)
CTVHS
28 tháng 6 2023
a) \(A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(A=x-\dfrac{1}{5}-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(A=\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)-\left(\dfrac{1}{5}+2-2\right)\)
\(A=-\dfrac{1}{5}\)
Vậy: ...
b) \(B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(B=\left[x^3-\left(2y\right)^3\right]-\left[x^3-\left(2y\right)^3\right]-10\)
\(B=-10\)
Vậy: ...
c) \(4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x+1\right)\left(x-1\right)-4x\)
\(=4\left(x^2+2x+4\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=\left(4x^2+4x^2-8x^2\right)+\left(8x-4x-4x\right)+\left(4+1+8\right)\)
\(=13\)
Vậy:...
AH
Akai Haruma
Giáo viên
20 tháng 6 2021
1. a
$(3x+5)^2=(3x)^2+2.3x.5+5^2$
$=9x^2+30x+25$
1.b
$(6x^2+\frac{1}{3})^2=(6x^2)^2+2.6x^2.\frac{1}{3}+(\frac{1}{3})^2$
$=36x^4+4x^2+\frac{1}{9}$
1.c
$(5x-4y)^2=(5x)^2-2.5x.4y+(4y)^2$
$=25x^2-40xy+16y^2$
1.d
(2x^2y-3y^3x)^2=(2x^2y)^2-2.2x^2y.3y^3x+(3y^3x)^2$
$=4x^4y^2-12x^3y^4+9x^2y^6$
AH
Akai Haruma
Giáo viên
20 tháng 6 2021
1.e
$(5x-3)(5x+3)=(5x)^2-3^2=25x^2-9$
1.f
$(6x+5y)(6x-5y)=(6x)^2-(5y)^2=36x^2-25y^2$
1.g
$(-4xy-5)(5-4xy)=(-4xy-5)(-4xy+5)$
$=(-4xy)^2-5^2=16x^2y^2-25$
1.h
$(a^2b+ab^2)(ab^2-a^2b)=(ab^2+a^2b)(ab^2-a^2b)$
$=(ab^2)^2-(a^2b)^2=a^2b^4-a^4b^2$
Giúp mình với mng ơi
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2021
\(3x^3y-12x^2y^2+6x^2y=3x^2y\left(x-4y+2\right)\)
\(\left(3x-2\right)^2-\left(x+1\right)^2=\left(3x-2-x-1\right)\left(3x-2+x+1\right)=\left(2x-3\right)\left(4x-1\right)\)
\(x^2+9x+14=x^2+2x+7x+14=x\left(x+2\right)+7\left(x+2\right)=\left(x+2\right)\left(x+7\right)\)
\(3x^2-14x+16=3x^2-6x-8x-16=3x\left(x-2\right)-8\left(x-2\right)=\left(3x-8\right)\left(x-2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2021
\(x^8+x+1\)
\(=\left(x^8-x^7+x^5-x^4+x^2\right)+\left(x^7-x^6+x^4-x^3+x\right)+x^6-x^5+x^3-x^2+1\)
\(=x^2\left(x^6-x^5+x^3-x^2+1\right)+x\left(x^6-x^5+x^3-x^2+1\right)+x^6-x^5+x^3-x^2+1\)
\(=\left(x^2+x+1\right)\left(x^6-x^5+x^3-x^2+1\right)\)
\(x^3-5x+2\)
\(=x^3+2x^2-x-2x^2-4x+2\)
\(=x\left(x^2+2x-1\right)-2\left(x^2+2x-1\right)\)
\(=\left(x-2\right)\left(x^2+2x-1\right)\)
2 tháng 7 2023
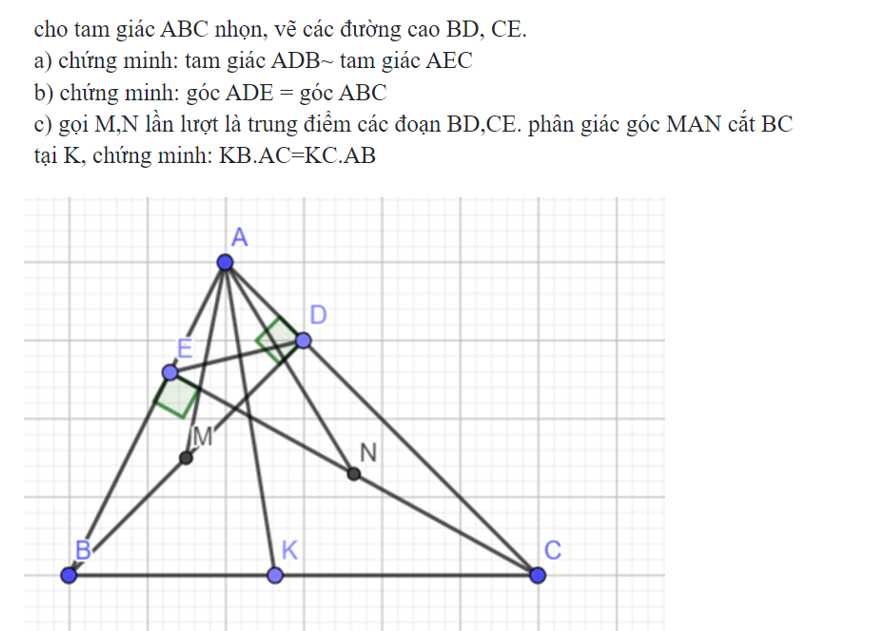
c: ΔABD đồng dạng với ΔACE
=>BD/CE=AB/AC
=>AB/AC=BM/CN
Xét ΔABM và ΔACN có
AB/AC=BM/CN
góc ABM=góc ACN
=>ΔABM đồng dạng với ΔACN
=>góc BAM=góc CAN
góc BAM+góc MAK=góc BAK
góc CAN+góc NAK=góc CAK
mà góc BAM=góc CAN và góc MAK=góc NAK
nên góc BAK=góc CAK
=>AK là phân giác của góc BAC
=>KB/AB=KC/AC
=>KB*AC=KC*AB
28 tháng 10 2021
Bài 2:
a: \(2\left(x-4\right)-x+3=0\)
\(\Leftrightarrow2x-8-x+3=0\)
hay x=5
b: \(x^2-25-\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=6\end{matrix}\right.\)
Bài 3:
\(-x^2-6x+2016\)
\(=-\left(x^2+6x-2016\right)\)
\(=-\left(x+3\right)^2+2025\le2025\forall x\)
Dấu '=' xảy ra khi x=-3