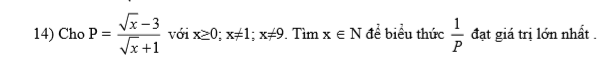Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


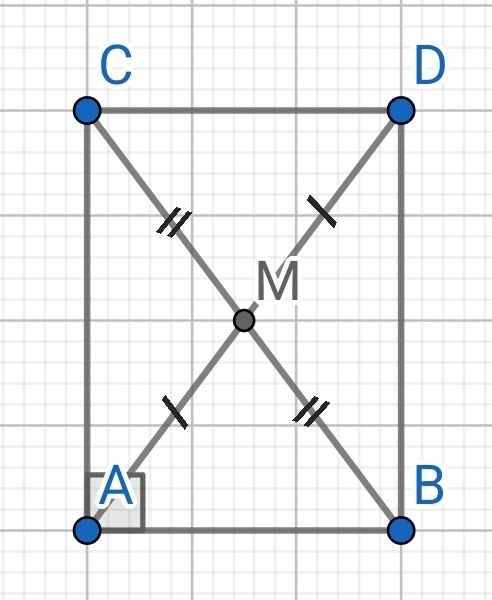
1: Xét ΔABD vuông tại A và ΔDAC vuông tại D có
góc ABD=góc DAC
=>ΔABD đồng dạng với ΔDAC
2: ΔABD đồng dạng với ΔDAC
=>BD/AC=AB/DA=AD/DC
=>AD/16=BD/AC=18/DA
=>AD^2=16*18=288
=>AD=12căn 2(cm)
AC=căn AD^2+DC^2=4căn 82(cm)


a) Do AM là đường trung tuyến của ∆ABC
⇒ M là trung điểm BC
Do MA = MD (gt)
⇒ M là trung điểm AD
Tứ giác ABDC có:
M là trung điểm BC (cmt)
M là trung điểm AD (cmt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (gt)
⇒ ABDC là hình chữ nhật
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC của ∆ABC
⇒ AM = BC : 2
= 10 : 2
= 5 (cm)
c) Nếu ∠B = 45⁰
⇒ C = 90⁰ - ∠B
= 90⁰ - 45⁰
= 45⁰
⇒ ∆ABC vuông cân tại A
⇒ AB = AC
Lại có ABDC là hình chữ nhật
⇒ ABDC là hình vuông

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)

1: Xét tứ giác AICK có
AI//CK
AI=CK
Do đó: AICK là hình bình hành
=>AK//CI
=>AE//IF
Xét tứ giác AIFE có IF//AE
nên AIFE là hình thang
2: Xét tứ giác BIDK có
BI//DK
BI=DK
Do đó: BIDK là hình bình hành
=>BD cắt IK tại trung điểm của mỗi đường
mà O là trung điểm của IK
nên O là trung điểm của BD
3:
AICK là hình bình hành
=>góc AIC=góc AKC
=>góc CIB=góc AKD
Xét ΔDEK và ΔBFI có
góc EKD=góc FIB
DK=BI
góc KDE=góc IBF
Do đó: ΔDEK=ΔBFI
4: Xét ΔADC có
DO,AK là trung tuyến
DO cắt AK tại E
=>E là trọng tâm
Xét ΔBAC có
BO,CI là trung tuyến
BO cắt CI tại F
Do đó: F là trọng tâm

Lời giải:
$x+y+z=0\Rightarrow x+y=-z$. Khi đó:
$x^2+y^2-z^2=(x+y)^2-2xy-z^2=(-z)^2-2xy-z^2=-2xy$
Tương tự: $y^2+z^2-x^2=-2yz, z^2+x^2-y^2=-2xz$
Khi đó:
$A=\frac{xy}{-2xy}+\frac{yz}{-2yz}+\frac{zx}{-2zx}=\frac{1}{-2}+\frac{1}{-2}+\frac{1}{-2}=\frac{-3}{2}$

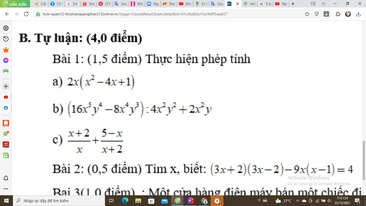
Bài 1:
a) 2x(x2 - 4x + 1)
= 2x3 - 8x2 + 2x
b) (16x5y4 - 8x4y3) : 4x2y2 + 2x2y
= 4x3y2 - 2x2y + 2x2y
= 4x3y2
c) \(\dfrac{x+2}{x}\) + \(\dfrac{5-x}{x+2}\)
= \(\dfrac{\left(x+2\right)^2+x\left(5-x\right)}{x\left(x+2\right)}\)
= \(\dfrac{x^2+4x+4+5x-x^2}{x\left(x+2\right)}\)
= \(\dfrac{4+9x}{x\left(x+2\right)}\)
Bài 2:
(3x + 2)(3x - 2) - 9x(x - 1) = 4
9x2 - 4 - 9x2 + 9x = 4
9x = 8
x = \(\dfrac{8}{9}\)

5.
\(A=\dfrac{2\sqrt{x}}{x-2\sqrt{x}+4}\)
\(\Leftrightarrow Ax-2A\sqrt{x}+4A=2\sqrt{x}\)
\(\Leftrightarrow Ax-2A\sqrt{x}+4A=2\sqrt{x}\)
\(\Leftrightarrow Ax-2\left(A-1\right)\sqrt{x}+4A=0\)
\(\Delta'=A^2-2A+1-4A^2=-3A^2-2A+1\ge0\)
\(\Leftrightarrow\left(1-3A\right)\left(A+1\right)\ge0\)
\(\Leftrightarrow-1\le A\le\dfrac{1}{3}\)
\(A=0\left(\text{vì }A\ge0\right)\Leftrightarrow x=0\)

\(a,S_{kính}=2\left(1,2+0,8\right).0,6+1,2.0,8=4,08\left(m^2\right)\\ b,S_{đáy}=1,2.0,8=0,96\left(m^2\right)\\ h=\dfrac{0,48}{0,96}=0,5\left(m\right)\)










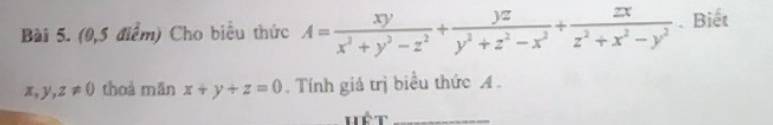
 giúp tôi với đi mọi người
giúp tôi với đi mọi người