
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


còn cái bài hình nãy mk làm ra r nhưng máy đơ k gửi đc câu trả lời nên k làm lại nữa
bài 15p trước câu hỏi tương tự có bài gần giống đấy

1/(x-1)x + 1/x(x+1) + 1/(x+1)(x+2) = 3/4
<=> 1/x-1 - 1/x + 1/x - 1/x+1 + 1/x+1 - 1/x+2 = 3/4
<=> 1/x-1 -1/x+2 = 3/4
<=> (x+2-x+1) / (x-1)(x+2) = 3/4
<=> 3/(x^2+x-2) = 3/4
<=> x^2+x-2=4
<=> x^2+x-6=0
<=> x=2 hoặc x= -3
=> nghiệm nhỏ nhất là -3

`[x+4]/5-x+4=x/3-[x-2]/2`
`<=>[6(x+4)-30(x-4)]/30=[10x-15(x-2)]/30`
`<=>6x+24-30x+120=10x-15x+30`
`<=>6x-30x-10x+15x=30-24-120`
`<=>-19x=-114`
`<=>x=6`
Vậy `S={6}`
\(\dfrac{x+4}{5}-x+4=\dfrac{x}{3}-\dfrac{x-2}{2}\)
\(\Leftrightarrow\dfrac{6\left(x+4\right)+30\left(4-x\right)}{30}=\dfrac{10x-15\left(x-2\right)}{30}\)
\(\Leftrightarrow6\left(x+4\right)+30\left(4-x\right)=10x-15\left(x-2\right)\)
\(\Leftrightarrow6x+24+120-30x=10x-15x+30\)
\(\Leftrightarrow-19x=-114\)
\(\Leftrightarrow x=6\)
Vậy \(S=\left\{6\right\}\)

Bài 1:
a) 2x(x2 - 4x + 1)
= 2x3 - 8x2 + 2x
b) (16x5y4 - 8x4y3) : 4x2y2 + 2x2y
= 4x3y2 - 2x2y + 2x2y
= 4x3y2
c) \(\dfrac{x+2}{x}\) + \(\dfrac{5-x}{x+2}\)
= \(\dfrac{\left(x+2\right)^2+x\left(5-x\right)}{x\left(x+2\right)}\)
= \(\dfrac{x^2+4x+4+5x-x^2}{x\left(x+2\right)}\)
= \(\dfrac{4+9x}{x\left(x+2\right)}\)
Bài 2:
(3x + 2)(3x - 2) - 9x(x - 1) = 4
9x2 - 4 - 9x2 + 9x = 4
9x = 8
x = \(\dfrac{8}{9}\)

\(3x^2-11x+6=0\)
\(\Leftrightarrow3x^2-9x-2x+6=0\)
\(\Leftrightarrow3x\left(x-3\right)-2\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\3x-2=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=3\\x=\frac{2}{3}\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{3;\frac{2}{3}\right\}\)
\(3x^2-11x+6=0\)
(=)\(x^2-\frac{2}{3}x-3x+2\)
(=) \(\left(x-3\right)\left(x-\frac{2}{3}\right)\)
(=)\(\hept{\begin{cases}x-3=0\\x-\frac{2}{3}=0\end{cases}}\)
(=)\(\hept{\begin{cases}x=3\\x=\frac{2}{3}\end{cases}}\)
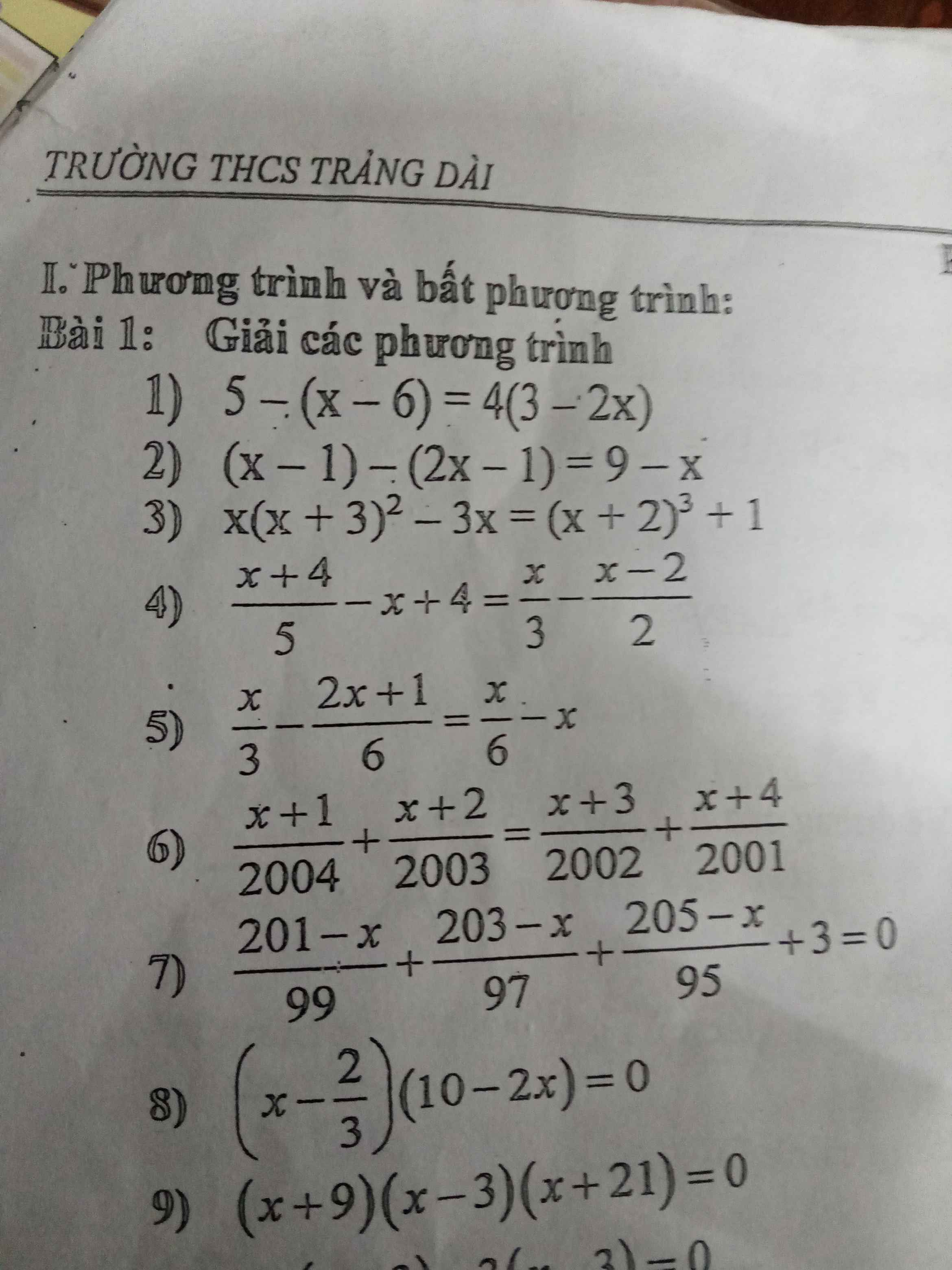
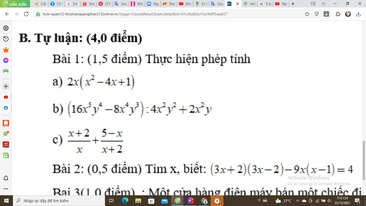 giúp tôi với đi mọi người
giúp tôi với đi mọi người
Answer:
\(y^2-25-\left(y+5\right)=0\)
\(\Rightarrow y^2-5^2-\left(y+5\right)=0\)
\(\Rightarrow\left(y-5\right).\left(y+5\right)-\left(y+5\right)=0\)
\(\Rightarrow\left(y+5\right).[\left(y-5\right)-1]=0\)
\(\Rightarrow\left(y+5\right).\left(y-6\right)=0\)
\(\Rightarrow\orbr{\begin{cases}y+5=0\\y-6=0\end{cases}}\Rightarrow\orbr{\begin{cases}y=5\\y=-6\end{cases}}\)
\(y^4-2y^3+10y^2-20y=0\)
\(\Rightarrow\left(y^4-2y^3\right)+\left(10y^2-20y\right)=0\)
\(\Rightarrow y^3.\left(y-2\right).\left(y^3+10y\right)=0\)
\(\Rightarrow y.\left(y-2\right).\left(y^2+10\right)=0\)
Trường hợp 1: \(y=0\)
Trường hợp 2: \(y-2=0\Rightarrow y=2\)
Trường hợp 3: \(y^2+10=0\Rightarrow y^2=-10\) (Loại)