ND
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SX
1
10 tháng 10 2015
(x³ - 4x² - 3x² + 12x + 2x - 8 =0
x²(x - 4) - 3x(x - 4) + 2(x - 4) =0
(x - 4)(x² - 3x + 2) =0
(x - 4)(x - 1)(x - 2) =0
=>X-4=0 hoặc x-1=0 hoặc x-2=0
(tự giải tiếp nhá)
NT
Giải phương trình 2-x/2009-1=1-x/2010-x/2011
P/S: Ai giúp tôi dc bài toán này cái ạ. Tôi đang cần gấp
4
18 tháng 2 2017
A=|x - 2009| + |x - 2010| + |x - 2011|
*TH1: Xét x ≤ 2009 ; khi đó
. A = 2009 - x + 2010 - x + 2011 -x
. A = 6030 - 3x
có x ≤ 2009 --> -x ≥ -2009 --> -3x ≥ -6027 --> 6030 - 3x ≥ 3
Dấu " = " <=> x = 2009
--> Amin = 3 <=> x = 2009
*TH2 : Xét 2009 < x ≤ 2010 ; ta có
. A = x - 2009 + 2010 - x + 2011 - x
. A = 2012 - x
có x ≤ 2010 --> -x ≥ -2010 --> 2012 - x ≥ 2
--> Amin = 2 <=> x = 2010
*TH3 : Xét 2010 < x < 2011 ; ta có :
. A = x - 2009 + x - 2010 + 2011 - x
. A = x - 8 > 2010 - 8 = 2002 --> không có min
*TH4 : Xét x ≥ 2011 ; ta có :
. A = x - 2009 + x - 2010 + x - 2011
. A = 3x - 6030 ≥ 3.1011 - 6030 = 3
Dấu " = " <=> xảy ra <=> x = 2011
--> Amin = 3 <=> x = 2011
** Kết hợp các trường hợp trên lại ta có :
Amin = 2 <=> x = 2010
HN
1
16 tháng 6 2023
1: Xét ΔABD vuông tại A và ΔDAC vuông tại D có
góc ABD=góc DAC
=>ΔABD đồng dạng với ΔDAC
2: ΔABD đồng dạng với ΔDAC
=>BD/AC=AB/DA=AD/DC
=>AD/16=BD/AC=18/DA
=>AD^2=16*18=288
=>AD=12căn 2(cm)
AC=căn AD^2+DC^2=4căn 82(cm)
MD
3
2
11 tháng 5 2022
`[x+4]/5-x+4=x/3-[x-2]/2`
`<=>[6(x+4)-30(x-4)]/30=[10x-15(x-2)]/30`
`<=>6x+24-30x+120=10x-15x+30`
`<=>6x-30x-10x+15x=30-24-120`
`<=>-19x=-114`
`<=>x=6`
Vậy `S={6}`
11 tháng 5 2022
\(\dfrac{x+4}{5}-x+4=\dfrac{x}{3}-\dfrac{x-2}{2}\)
\(\Leftrightarrow\dfrac{6\left(x+4\right)+30\left(4-x\right)}{30}=\dfrac{10x-15\left(x-2\right)}{30}\)
\(\Leftrightarrow6\left(x+4\right)+30\left(4-x\right)=10x-15\left(x-2\right)\)
\(\Leftrightarrow6x+24+120-30x=10x-15x+30\)
\(\Leftrightarrow-19x=-114\)
\(\Leftrightarrow x=6\)
Vậy \(S=\left\{6\right\}\)
TL
0
TL
1
2 tháng 2 2017
b) nhẩm đưuọc nghiệm x=1
\(\Leftrightarrow\left(x-1\right)\left(x^2-5x+6\right)=0\Rightarrow\orbr{\begin{cases}x=1\\x^2-5x+6\left(2\right)\end{cases}}\)
\(\left(2\right)\Leftrightarrow\left(x-2\right)\left(x-3\right)\Rightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}\) KL x=1,2,3
c)
(x^2+3x+1)^2=x^4+9x^2+1+6x^3+2x^2+6x (nhân pp dẽ hơn ghép)
\(\orbr{\begin{cases}x=\frac{3-\sqrt{5}}{2}\\x=\frac{3+\sqrt{5}}{2}\end{cases}}\)
29 tháng 3 2017
a) 2x3+5x2-3x=0
<=> 2x3+6x2-x2-3x=0
<=> 2x2(x+3)-x(x+3)=0
<=> (x+3)(2x2-x)=0
<=> (x+3)x(2x-1)=0
\(\Rightarrow\left\{{}\begin{matrix}x+3=0\\x=0\\2x-1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy ...
c) x3+1=x(x+1)
<=> (x+1)(x2+1-x)-x(x+1)=0
<=> (x+1)(x2-2x+1)=0
<=> (x+1)(x-1)2=0
\(\Rightarrow\left\{{}\begin{matrix}x+1=0\\x-1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
Vậy ...
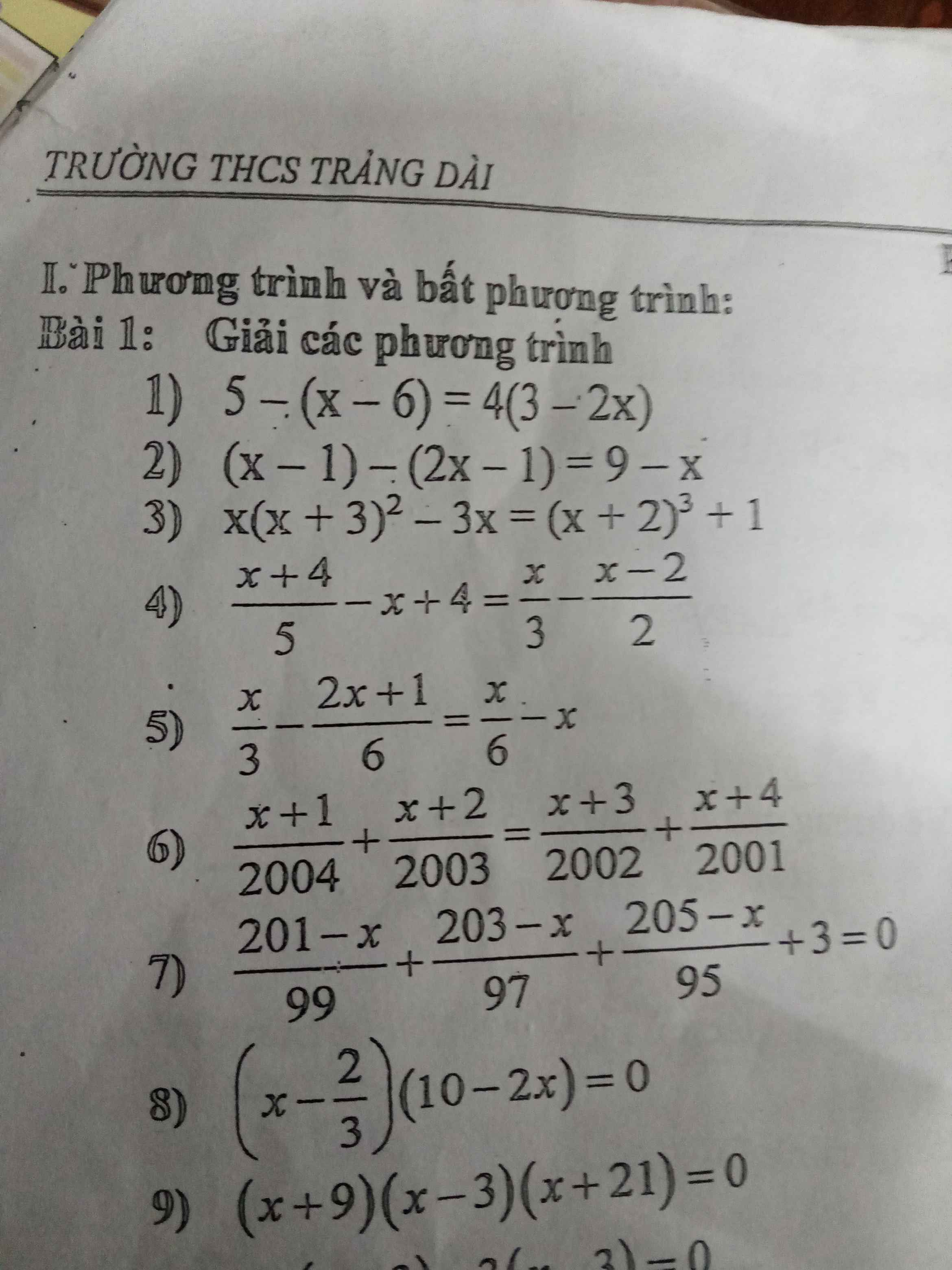
\(3x^2-11x+6=0\)
\(\Leftrightarrow3x^2-9x-2x+6=0\)
\(\Leftrightarrow3x\left(x-3\right)-2\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\3x-2=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=3\\x=\frac{2}{3}\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{3;\frac{2}{3}\right\}\)
\(3x^2-11x+6=0\)
(=)\(x^2-\frac{2}{3}x-3x+2\)
(=) \(\left(x-3\right)\left(x-\frac{2}{3}\right)\)
(=)\(\hept{\begin{cases}x-3=0\\x-\frac{2}{3}=0\end{cases}}\)
(=)\(\hept{\begin{cases}x=3\\x=\frac{2}{3}\end{cases}}\)