K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 10 2023
d) \(\dfrac{1}{x^4y^6z};\dfrac{2}{3x^2y^7z^2};\dfrac{3}{4x^5y}\)
Mẫu thức chung: \(12x^5y^7z^2\)
Quy đồng mẫu thức các phân thức ta được:
\(\dfrac{12xyz}{12x^5y^7z^2};\dfrac{8x^3}{12x^5y^7z^2};\dfrac{9y^6z^2}{12x^5y^7z^2}\)
9 tháng 12 2023
c: \(\dfrac{2x}{x+5}+\dfrac{10x}{x^2+5x}\)
\(=\dfrac{2x}{x+5}+\dfrac{10x}{x\left(x+5\right)}\)
\(=\dfrac{2x}{x+5}+\dfrac{10}{x+5}=\dfrac{2x+10}{x+5}=\dfrac{2\left(x+5\right)}{x+5}=2\)
d: \(\dfrac{x}{x^2-36}+\dfrac{x-6}{x^2+6x}+\dfrac{-36}{\left(x^2-6x\right)\left(x+6\right)}\)
\(=\dfrac{x}{\left(x-6\right)\left(x+6\right)}+\dfrac{x-6}{x\left(x+6\right)}+\dfrac{-36}{x\left(x-6\right)\left(x+6\right)}\)
\(=\dfrac{x^2+\left(x-6\right)^2-36}{x\left(x-6\right)\left(x+6\right)}\)
\(=\dfrac{x^2+x^2-12x+36-36}{x\left(x-6\right)\left(x+6\right)}=\dfrac{2x^2-12x}{x\left(x-6\right)\left(x+6\right)}\)
\(=\dfrac{2\left(x^2-6x\right)}{\left(x^2-6x\right)\left(x+6\right)}=\dfrac{2}{x+6}\)
QN
3
5 tháng 9 2021
\(a,A=x^2-6x-2=\left(x-3\right)^2-11\ge-11\)
Dấu \("="\Leftrightarrow x=3\)
\(b,B=6x-9x^2+2=-\left(3x-1\right)^2+3\le3\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{3}\)
H9
HT.Phong (9A5)
CTVHS
30 tháng 6 2023
a) \(\left(2x+3\right)\left(4x^2-6x+9\right)-2\left(4x^3-1\right)\)
\(=\left(2x+3\right)\left[\left(2x\right)^2-2x\cdot3+3^2\right]-2\left(4x^3-1\right)\)
\(=\left[\left(2x\right)^3+3^3\right]-2\left(4x^3-1\right)\)
\(=\left(8x^3+27\right)-8x^3+2\)
\(=8x^3+27-8x^3+2\)
\(=29\)
Vậy: ....
c) \(2\left(x^3+y^3\right)-3\left(x^3+y^3\right)\)
\(=2\left(x+y\right)\left(x^2-xy+y^2\right)-3x^2-3y^2\)
\(=2\left(x^2-xy+y^2\right)\cdot1-3x^2-3y^2\)
\(=2x^2-2xy+2y^2-3x^2-3y^2\)
\(=-x^2-2xy-y^2\)
\(=-\left(x^2+2xy+y^2\right)\)
\(=-\left(x+y\right)^2\)
\(=-\left(1\right)^2=-1\)
Vậy: ...
8 tháng 8 2023
4.2:
a: x^2-x+1=x^2-x+1/4+3/4
=(x-1/2)^2+3/4>=3/4>0 với mọi x
=>x^2-x+1 ko có nghiệm
b: 3x-x^2-4
=-(x^2-3x+4)
=-(x^2-3x+9/4+7/4)
=-(x-3/2)^2-7/4<=-7/4<0 với mọi x
=>3x-x^2-4 ko có nghiệm
5:
a: x^2+y^2=25
x^2-y^2=7
=>x^2=(25+7)/2=16 và y^2=16-7=9
x^4+y^4=(x^2)^2+(y^2)^2
=16^2+9^2
=256+81
=337
b: x^2+y^2=(x+y)^2-2xy
=1^2-2*(-6)
=1+12=13
x^3+y^3=(x+y)^3-3xy(x+y)
=1^3-3*1*(-6)
=1+18=19
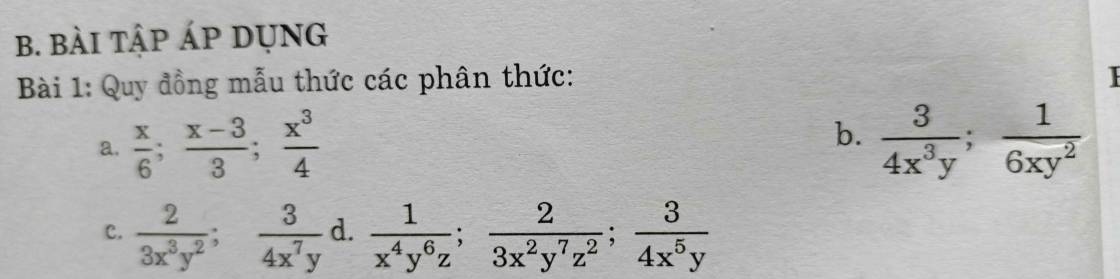
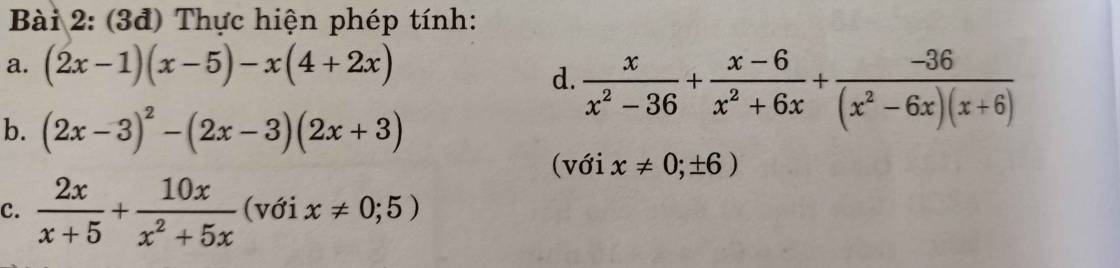
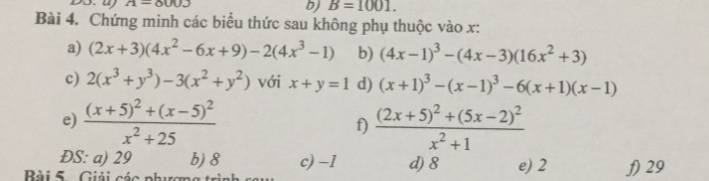
\(E=4x^4+52x^3+171x^2+13x-30\)
\(E=4x^4+24x^3+28x^3+168x^2+3x^2+18x-5x-30\)
\(E=4x^3\left(x+6\right)+28x^2\left(x+6\right)+3x\left(x+6\right)-5\left(x+6\right)\)
\(E=\left(4x^3+28x^2+3x-5\right)\left(x+6\right)\)
\(E=\left(4x^3+2x^2+26x^2+13x-10x-5\right)\left(x+6\right)\)
\(E=\left[2x^2\left(2x+1\right)+13x\left(2x+1\right)-5\left(2x+1\right)\right]\left(x+6\right)\)
\(E=\left(2x^2+13x-5\right)\left(2x+1\right)\left(x+6\right)\)
\(D=4\left(x^2+11x+30\right)\left(x^2+22x+120\right)-3x^2\)
\(D=4\left(x+5\right)\left(x+6\right)\left(x+10\right)\left(x+12\right)-3x^2\)
\(D=4\left(x^2+17x+60\right)\left(x^2+16x+60\right)-3x^2\)
đặt \(x^2+17x+60=a\)
\(D=4\left(a-x\right)a-3x^2\)
\(D=4a^2-4ax-3x^2\)
đến đây bí