K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 2 2022
1: Thay \(x=\dfrac{4-\sqrt{7}}{2}\) vào B, ta được:
\(B=\dfrac{1}{\sqrt{\dfrac{4-\sqrt{7}}{2}}+1}=1:\left(\dfrac{\sqrt{7}-1+2}{2}\right)=1\cdot\dfrac{2}{\sqrt{7}+1}=\dfrac{-1+\sqrt{7}}{3}\)
17 tháng 2 2022
1: Thay \(x=4-2\sqrt{3}\) vào Q, ta được:
\(Q=\dfrac{\sqrt{3}-1+1}{\sqrt{3}-1-3}=\dfrac{\sqrt{3}}{\sqrt{3}-4}=\dfrac{-3-4\sqrt{3}}{13}\)
2: \(P=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{-3\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(M=P+Q=\dfrac{-3\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\dfrac{-3\sqrt{x}-3+x+4\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
AM
28 tháng 1 2022
Với m=-2
Phương trình tọa độ giao điểm của (d) và (P) là:
\(2x^2=\left(-2-3\right)x+\left(-2\right)\Leftrightarrow2x^2+5x+2=0\Leftrightarrow\)\(\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-2\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=\dfrac{1}{2}\\y=8\end{matrix}\right.\)
Gọi \(M\left(-\dfrac{1}{2};\dfrac{1}{2}\right),N\left(-2;8\right)\) và kẻ \(NH\perp MO\) ta có hình vẽ như sau:
Gọi phương trình đường thẳng MO là: ax+b=y
\(\left\{{}\begin{matrix}a.0+b=0\\-2a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=-4\end{matrix}\right.\)
Phương trình đường thẳng MO là: -4x=y
Gọi phương trình đường thẳng NH là: ax+b=y
Để NH vuông góc với MO thì: a.a'=-1 \(\Leftrightarrow a.\left(-4\right)=-1\Leftrightarrow a=\dfrac{1}{4}\)
Ta có: \(y=\dfrac{1}{4}x+b\Leftrightarrow\dfrac{1}{2}=\dfrac{1}{4}.\dfrac{-1}{2}+b\Rightarrow b=\dfrac{5}{8}\)
Phương trình đường thẳng NH là: \(y=\dfrac{1}{4}x+\dfrac{5}{8}\)
Phương trình tọa độ giao điểm của NH và MO là: \(-4x=\dfrac{1}{4}x+\dfrac{5}{8}\Leftrightarrow x=\dfrac{-5}{34}\Rightarrow y=\dfrac{10}{17}\)
Độ dài đoạn NH là: NH= \(\sqrt{\left(-\dfrac{5}{34}--\dfrac{1}{2}\right)^2+\left(\dfrac{10}{17}-\dfrac{1}{2}\right)^2}=\dfrac{3\sqrt{17}}{34}\)
Độ dài đoạn MO là: MO=\(\sqrt{\left(-2-0\right)^2+\left(8-0\right)^2}=2\sqrt{17}\)
Diện tích tam giác OMN là: \(S=\dfrac{1}{2}NH.OM=\dfrac{1}{2}.\dfrac{3\sqrt{17}}{34}.2\sqrt{17}\)=1,5(đvdt)
2 tháng 3 2022
1: Thay x=16 vào A, ta được:
\(A=\dfrac{4-1}{4+3}=\dfrac{3}{7}\)
2: \(P=A:B\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+3}:\dfrac{x-3\sqrt{x}-x-6\sqrt{x}-9+x+11\sqrt{x}+6}{x-9}\)
\(=\dfrac{\sqrt{x}-1}{1}\cdot\dfrac{\sqrt{x}-3}{x+2\sqrt{x}-3}=\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)
4 tháng 6 2023
b: kẻ đường kính AD
góc ACD=90 độ=góc ABD
=>AC vuông góc CD và AB vuông góc BD
=>BH//CD và CH//BD
=>BDCH là hbh
=>H,N,D thẳng hàng và N là trung điểm của HD
=>NT là đường trung bình của ΔAHD
=>NT//AD và NT=1/2AD=OA
=>NT//OA
=>ATNO là hbh
EN=1/2BC
=>EN=BN
=>ΔNEB cân tại N
=>góc NBE=góc NEB
EJ=1/2AH=JH
=>ΔJEH cân tại J
=>góc JEH=góc JHE
góc NBE+Góc ACB=90 độ
góc HAC+góc ACB=90 độ
=>góc NBE=góc HAC
mà góc JHE+góc HAC=90 độ
nên góc JHE+góc NBE=90 độ
=>góc JEN=90 độ
27 tháng 2 2022
Hướng dẫn:
Ta có:
\(x^2-xy+y^2=2x-3y-2\)
\(\Leftrightarrow2x^2-2xy+2y^2-4x+6y+4+9=9\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2-4x+4\right)+\left(y^2+6y+9\right)=9\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x-2\right)^2+\left(y+3\right)^2=9\)
Xét....
Đây là 1 cách nhưng làm hơi dài.
27 tháng 2 2022
\(x^2-xy+y^2=2x-3y-2\\ \Leftrightarrow x^2-xy+y^2-2x+3y+2=0\left(1\right)\\ \Leftrightarrow x^2-x\left(y+2\right)+y^2+3y+2=0\)
Coi đây là pt bậc 2 ẩn x
Ta có: \(\Delta=\left[-\left(y+2\right)\right]^2-4\left(y^2+3y+2\right)=y^2+4y+4-4y^2-12y-8=-3y^2-8y-4\)
Để pt có nghiệm nguyên thì \(\Delta\ge0\Leftrightarrow-3y^2-8y-4\ge0\Leftrightarrow-2\le y\le-\dfrac{2}{3}\)
\(\Leftrightarrow y\in\left\{-2;-1\right\}\)
Thay y=-2 vào (1) ta có:
\(\left(1\right)\Leftrightarrow x^2-x.\left(-2\right)+\left(-2\right)^2-2x+3.\left(-2\right)+2=0\\ \Leftrightarrow x^2+2x+4-2x-6+2=0\\ \Leftrightarrow x^2=0\Leftrightarrow x=0\)
Thay y=-1 vào pt ta có:
\(\left(1\right)\Leftrightarrow x^2-x.\left(-1\right)+\left(-1\right)^2-2x+3.\left(-1\right)+2=0\\ \Leftrightarrow x^2+x+1-2x-3+2=0\\ \Leftrightarrow x^2-x=0\\ \Leftrightarrow x\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(\left(x,y\right)\in\left\{\left(0;-2\right);\left(0;-1\right);\left(1;-1\right)\right\}\)
VT
Vũ Thị Minh Ánh
Giáo viên
29 tháng 12 2022
\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
\(\Leftrightarrow3\sqrt{x-2}-2\sqrt{x-2}+3\sqrt{x-2}=40\)
\(\Leftrightarrow\sqrt{x-2}=10\)
\(\Leftrightarrow x-2=100\)
\(\Leftrightarrow x=102\)
26 tháng 1 2022
a: Khi m=-2 thì (d): y=-5x-2
ii: Tọa độ giao điểm của (P) và (d) là:
\(\left\{{}\begin{matrix}2x^2+5x+2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{-\dfrac{1}{2};-2\right\}\\y\in\left\{\dfrac{1}{2};8\right\}\end{matrix}\right.\)
Vậy: M(-1/2;1/2); N(-2;8)
\(OM=\sqrt{\left(-\dfrac{1}{2}-0\right)^2+\left(\dfrac{1}{2}-0\right)^2}=\sqrt{\dfrac{1}{4}+\dfrac{1}{4}}=\dfrac{\sqrt{2}}{2}\)
\(ON=\sqrt{\left(-2-0\right)^2+\left(8-0\right)^2}=2\sqrt{17}\)
\(MN=\sqrt{\left(-2+\dfrac{1}{2}\right)^2+\left(8-\dfrac{1}{2}\right)^2}=\sqrt{\dfrac{9}{4}+\dfrac{225}{4}}=\dfrac{3\sqrt{26}}{2}\)
\(P=OM+ON+NM\simeq4,93\left(cm\right)\)
\(S=\sqrt{4,93\cdot\left(4,93-\dfrac{\sqrt{2}}{2}\right)\cdot\left(4.93-2\sqrt{17}\right)\left(4.93-\dfrac{3\sqrt{26}}{2}\right)}=13,7\left(cm^2\right)\)
14 tháng 1 2022
a: \(\Leftrightarrow\left\{{}\begin{matrix}6x=-12\\x-2y=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\2y=x+8=-2+8=6\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(-2;3\right)\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}x-2y=5\\x-2y=5\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in R\)
c: \(\Leftrightarrow\left\{{}\begin{matrix}3x-3y=9\\3x-3y=1\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)
d: \(\Leftrightarrow\left\{{}\begin{matrix}-5y=5\\3x+y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=0\end{matrix}\right.\)
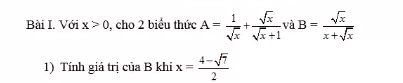
i don't know