K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CT
18
P
Phong
CTVHS
17 tháng 8 2023
Ta có các quy luật sau:
\(\left(1+3\right)-2=2\)
\(\left(2+2\right)-3=1\)
\(\left(5+5\right)-6=4\)
Vậy dòng cuối là:
\(\left(5+9\right)-5=9\)
Số điền vào là 9
(Quy luật: lấy 2 số phía dưới cộng với nhau rồi trừ cho số phía trên sẽ ra được số ở giữa)
CT
6
NV
11 tháng 8 2023
Quy luật: Hiệu của số lớn hơn trừ cho số nhỏ hơn trong mổi ô chính là kết quả của ô màu vàng đối diện
17-13=4
15-6=9
14-8=6
19-12=7
23-15=8
27-25=2
23-18=5
Suy ra: 12-x=3
=> x=12-3=9
Đáp án C
11 tháng 8 2023
Giải thích: Mỗi số trong hình tam giác màu vàng bằng số lớn hơn của hình bình hành đối diện trừ đi số bé hơn ở hình bình hành đối diện.
=> ? - 12 = 3 hoặc 12 - ? = 3
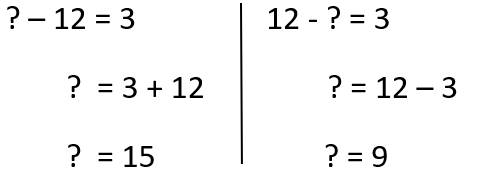
=> Đáp án là 15 hoặc 9
Đáp án: c
Bổ sung: Đáp án cũng có thể là 15
20 tháng 8
1: 2⋮x
mà x là số tự nhiên
nên x∈{1;2}
2: 2⋮x+1
=>x+1∈{1;-1;2;-2}
=>x∈{0;-2;1;-3}
mà x>=0
nên x∈{0;1}
3: 2⋮x+2
mà x+2>=2(Do x là số tự nhiên)
nên x+2=2
=>x=0
4: 2⋮x-1
=>x-1∈{1;-1;2;-2}
=>x∈{2;0;3;-1}
mà x>=0
nên x∈{0;2;3}
5: 2⋮x-2
=>x-2∈{1;-1;2;-2}
=>x∈{3;1;4;0}
6: 2⋮2-x
=>2⋮x-2
=>x-2∈{1;-1;2;-2}
=>x∈{3;1;4;0}
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
20 tháng 8
Bài 1:
2 ⋮ \(x\)(\(x\) ∈ N*)
2 ⋮ \(x\)
⇒ \(x\) ∈ Ư(2) = {-2; -1; 1; 2}
Vì \(x\) ∈ N* nên \(x\) ∈ {1; 2}
Vậy \(x\) ∈ {1; 2}
ứng với $3$ học sinh.
24 tháng 4 2023
a) Có 18 học sinh đi đến trường bằng xe đạp.
b) Lớp 6A có 45 học sinh.
c) Tỉ số phần trăm học sinh đi bộ đến trường là:
(9 : 45) . 100 = 20%
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
23 tháng 8
Câu 6:
2\(xy\) - 5 = y - 2\(x\)
2\(xy\) + 2\(x\) = 5 + y
\(x\)(2y + 2) = 5 + y
\(x\) = \(\frac{5+y}{2y+2}\)
\(x\) ∈ Z ⇔ (5+ y) ⋮ (2y + 2)
(10 + 2y) ⋮ (2y + 2)
[(2y+ 2) + 8] ⋮ (2y+ 2)
8 ⋮ (2y+ 2)
(2y+ 2) ∈ Ư(8) = {-8; -4; -2; - 1; 1; 2; 4; 8}
Lập bảng ta có:
2y+2 | -8 | -4 | -2 | -1 | 1 | 2 | 4 | 8 |
y | -5 | -3 | -2 | -3/2 | 1/2 | 0 | 1 | 3 |
\(x=\frac{5+y}{2y+2}\) | 0 | -1/2 | -3/2 | 5/4 | 3/2 | 1 | ||
\(x;y\in Z\) | ktm | ktm | ktm | ktm | ktm | tm |
Theo bảng trên ta có: (\(x;y\)) = (0; -5); (1; 3)
KD
23 tháng 8
2xy - 5 = y - 2x
2xy - y + 2x =5
2x( y+1 ) - y =5
2x( y+1 ) - ( y+1 ) = 5-1
(2x+1)(y+1) = 4
Vì x,y là số nguyên nên:
2x+1 là số nguyên lẻ
y+1 là số nguyên.
Tá có:
4= 1.4 = 4.1 =2.2 = (-1)(-4) = (-4)(-1) = (-2)(-2)
TH1:
2x+1=1
y+1=4
=> x=0 ; y=3 (Thoả mãn)
Tương tự với các TH khác...
9 tháng 9
1: \(1026-\left\lbrack\left(3^4+1\right):41\right\rbrack\)
\(=1026-82:41\)
=1026-2
=1024
\(2^{11}:\left\lbrace1026-\left\lbrack\left(3^4+1\right):41\right\rbrack\right\rbrace\)
\(=2^{11}:2^{10}=2\)
2: \(250:\left\lbrace1500:\left\lbrack4\cdot5^3-2^3\cdot25\right\rbrack\right\rbrace\)
\(=250:\left\lbrace1500:\left\lbrack4\cdot125-8\cdot25\right\rbrack\right\rbrace\)
\(=250:\left\lbrace1500:\left\lbrack500-200\right\rbrack\right\rbrace=250:\frac{1500}{3}=250:500=0,5\)
3: \(12+3\cdot\left\lbrace90:\left\lbrack39-\left(2^3-5\right)^2\right\rbrack\right\rbrace\)
\(=12+3\cdot\left\lbrace90:\left\lbrack39-\left(8-5\right)^2\right\rbrack\right\rbrace\)
\(=12+3\cdot\left\lbrace90:\left\lbrack39-3^2\right\rbrack\right\rbrace\)
\(=12+3\cdot\left\lbrace90:\left\lbrack39-9\right\rbrack\right\rbrace\)
\(=12+3\cdot\left\lbrace90:30\right\rbrace=12+3\cdot3=21\)
4: \(24:\left\lbrace390:\left\lbrack500-\left(5^3+49\cdot5\right)\right\rbrack\right\rbrace\)
\(=24:\left\lbrace390:\left\lbrack500-\left(125+245\right)\right\rbrack\right\rbrace\)
\(=24:\left\lbrace390:\left\lbrack500-125-245\right\rbrack\right\rbrace\)
\(=24:\left\lbrace390:\left\lbrack375-245\right\rbrack\right\rbrace\)
\(=24:\left\lbrace390:130\right\rbrace=\frac{24}{3}=8\)
5: \(117:\left\lbrace\left\lbrack79-3\cdot\left(3^3-17\right)\right\rbrack:7+2\right\rbrace\)
\(=117:\left\lbrace\left\lbrack79-3\cdot\left(27-17\right)\right\rbrack:7+2\right\rbrace\)
\(=117:\left\lbrace\left\lbrack79-3\cdot10\right\rbrack:7+2\right\rbrace\)
\(=117:\left\lbrace49:7+2\right\rbrace=\frac{117}{9}=13\)
6: \(514-4\cdot\left\lbrace\left\lbrack40+8\left(6-3\right)^2\right\rbrack-12\right\rbrace\)
\(=514-4\cdot\left\lbrace\left\lbrack40+8\cdot3^2\right\rbrack-12\right\rbrace\)
\(=514-4\cdot\left\lbrace\left\lbrack40+8\cdot9\right\rbrack-12\right\rbrace\)
\(=514-4\cdot\left\lbrace112-12\right\rbrace\)
\(=514-4\cdot100=514-400=114\)
7: \(25\cdot\left\lbrace32:\left\lbrack\left(12-4\right)+4\cdot\left(16:2^3\right)\right\rbrack\right\rbrace\)
\(=25\cdot\left\lbrace32:\left\lbrack8+4\cdot2\right\rbrack\right\rbrace\)
\(=25\cdot\left\lbrace32:16\right\rbrace=25\cdot2=50\)
8: \(30:\left\lbrace175:\left\lbrack355-\left(135+37\cdot5\right)\right\rbrack\right\rbrace\)
\(=30:\left\lbrace175:\left\lbrack355-\left(135+185\right)\right\rbrack\right\rbrace\)
\(=30:\left\lbrace175:\left\lbrack355-320\right\rbrack\right\rbrace=30:\left\lbrace175:35\right\rbrace=\frac{30}{5}=6\)
9: \(32:\left\lbrace160:\left\lbrack300-\left(175+21\cdot5\right)\right\rbrack\right\rbrace\)
\(=32:\left\lbrace160:\left\lbrack300-\left(175+105\right)\right\rbrack\right\rbrace\)
\(=32:\left\lbrace160:\left\lbrack300-280\right\rbrack\right\rbrace\)
\(=32:\left\lbrace160:20\right\rbrace=\frac{32}{8}=4\)
10: \(750:\left\lbrace130-\left\lbrack\left(5\cdot14-65\right)^3+3\right\rbrack\right\rbrace\)
\(=750:\left\lbrace130-\left\lbrack\left(70-65\right)^3+3\right\rbrack\right\rbrace\)
\(=750:\left\lbrace130-\left\lbrack5^3+3\right\rbrack\right\rbrace\)
\(=750:\left\lbrace130-128\right\rbrace=750:2=375\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
24 tháng 1 2024
\(\dfrac{15}{34}+\dfrac{1}{3}+\dfrac{19}{34}-\dfrac{4}{3}+\dfrac{3}{7}=\left(\dfrac{15}{34}+\dfrac{19}{34}\right)+\left(\dfrac{1}{3}-\dfrac{4}{3}\right)+\dfrac{3}{7}=1-1+\dfrac{3}{7}=\dfrac{3}{7}\)
23 tháng 8
Bài 8:
a: \(5^3=125;3^5=243\)
mà 125<243
nên \(5^3<3^5\)
b: \(7\cdot2^{13}<8\cdot2^{13}=2^3\cdot2^{13}=2^{16}\)
c: \(27^5=\left(3^3\right)^5=3^{3\cdot5}=3^{15}\)
\(243^3=\left(3^5\right)^3=3^{5\cdot3}=3^{15}\)
Do đó: \(27^5=243^5\)
d: \(625^5=\left(5^4\right)^5=5^{4\cdot5}=5^{20}\)
\(125^7=\left(5^3\right)^7=5^{3\cdot7}=5^{21}\)
mà 20<21
nên \(625^5<125^7\)
Bài 9:
a: \(3^{x}\cdot5=135\)
=>\(3^{x}=\frac{135}{5}=27=3^3\)
=>x=3(nhận)
b: \(\left(x-3\right)^3=\left(x-3\right)^2\)
=>\(\left(x-3\right)^3-\left(x-3\right)^2=0\)
=>\(\left(x-3\right)^2\cdot\left\lbrack\left(x-3\right)-1\right\rbrack=0\)
=>\(\left(x-3\right)^2\cdot\left(x-4\right)=0\)
=>\(\left[\begin{array}{l}x-3=0\\ x-4=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=3\left(nhận\right)\\ x=4\left(nhận\right)\end{array}\right.\)
c: \(\left(2x-1\right)^4=81\)
=>\(\left[\begin{array}{l}2x-1=3\\ 2x-1=-3\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=4\\ 2x=-2\end{array}\right.\Rightarrow\left[\begin{array}{l}x=2\left(nhận\right)\\ x=-1\left(loại\right)\end{array}\right.\)
d: \(\left(5x+1\right)^2=3^2\cdot5+76\)
=>\(\left(5x+1\right)^2=9\cdot5+76=45+76=121\)
=>\(\left[\begin{array}{l}5x+1=11\\ 5x+1=-11\end{array}\right.\Rightarrow\left[\begin{array}{l}5x=10\\ 5x=-12\end{array}\right.\Rightarrow\left[\begin{array}{l}x=2\left(nhận\right)\\ x=-\frac{12}{5}\left(loại\right)\end{array}\right.\)
e: \(5+2^{x-3}=29-\left\lbrack4^2-\left(3^2-1\right)\right\rbrack\)
=>\(2^{x-3}+5=29-\left\lbrack16-9+1\right\rbrack\)
=>\(2^{x-3}+5=29-8=21\)
=>\(2^{x-3}=16=2^4\)
=>x-3=4
=>x=4+3=7(nhận)
f: \(3+2^{x-1}=24-\left\lbrack4^2-\left(2^2-1\right)\right\rbrack\)
=>\(2^{x-1}+3=24-\left\lbrack16-4+1\right\rbrack=24-13=11\)
=>\(2^{x-1}=11-3=8=2^3\)
=>x-1=3
=>x=4(nhận)
Bài 6:
a: \(5\cdot5\cdot5\cdot5\cdot5\cdot5=5^6\)
b: \(27\cdot14\cdot7\cdot2=27\cdot14\cdot14=3^3\cdot14^2\)
c: \(x\cdot x\cdot x\cdot y=x^3\cdot y\)
d: \(5^3\cdot5^4=5^{3+4}=5^7\)
e: \(7^8:7^2=7^{8-2}=7^6\)
f: \(42^7:6^7\cdot49=7^7\cdot49=7^7\cdot7^2=7^{7+2}=7^9\)
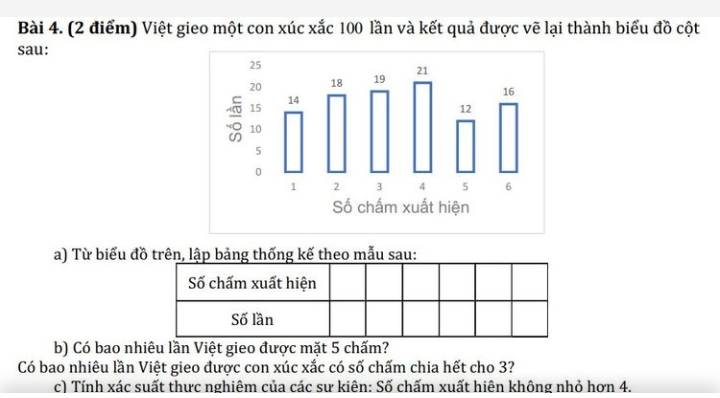
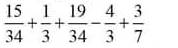
a)
b) - Có 12 lần Việt gieo xúc xắc được 5 điểm.
- Có 19 + 16 = 35 lần Việt gieo số chấm chia hết cho 3.
c) Xác suất thực nghiệm của số chấm xuất hiện không nhỏ hơn 4:
(21 + 12 + 16) : (14 + 18 + 19 + 21 + 12 + 16)
= 49 : 100
= 0,49