giúp mình vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
16
5 tháng 3 2022
Bài 2 :
Bài 2 :
a, \(A=6x^3y^6z\)hệ số 6 ; biến x^3y^6z ; bậc 10
b, \(B=-\dfrac{2}{3}xy^2\left(9x^4y^2\right)=-6x^5y^4\)
hệ số -6 ; biến x^5y^4 ; bậc 9
Bài 3 :
\(A=3,5xy^2\) ta có \(x=\left|-2\right|=2;y=-1\)
Thay vào ta đc
A = 3,5 . 2 . 1 = 7
10 tháng 5 2023
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>ME=MF
TH
1
30 tháng 12 2021
a: Xét ΔAMC và ΔBMD có
MA=MB
\(\widehat{AMC}=\widehat{BMD}\)
MC=MD
Do đó: ΔAMC=ΔBMD
AH
Akai Haruma
Giáo viên
6 tháng 9 2021
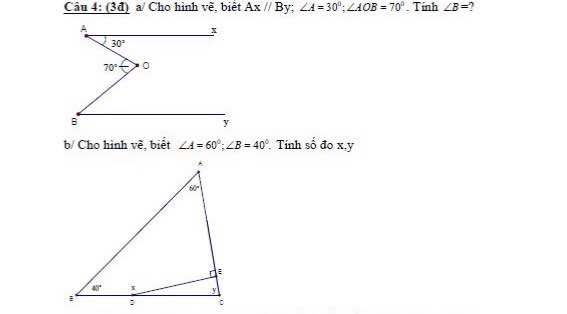
Câu 4a.
Kẻ tia $Om\parallel Ax$ như hình:
Vì $Ax\parallel Om$ nên $\widehat{AOm}=\widehat{xAO}=30^0$ (hai góc so le trong)
$\Rightarrow \widehat{mOB}=\widehat{AOB}-\widehat{AOm}=70^0-30^0=40^0$
$Ax\parallel By, Ax\parallel Om\Rightarrow By\parallel Om$
$\Rightarrow \widehat{B}=\widehat{mOB}=40^0$ (hai góc so le trong)
6 tháng 9 2021
a) Trên nửa mặt phẳng bờ OB chứa điểm A, kẻ tia Oz//Ax//By
Ta có: Oz//Ax(cách vẽ)
\(\Rightarrow\widehat{xAO}=\widehat{AOz}=30^0\)( 2 góc so le trong)
Ta có: \(\widehat{AOz}+\widehat{zOB}=\widehat{AOB}\)
\(\Rightarrow\widehat{zOB}=\widehat{AOB}-\widehat{AOz}=70^0-30^0=40^0\)
Ta có: Oz//By
\(\Rightarrow\widehat{B}=\widehat{zOB}=40^0\)( 2 góc so le trong)
b) Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)( tổng 3 góc trong tam giác)
\(\Rightarrow\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-60^0-40^0=80^0\)
\(\Rightarrow y=80^0\)
Xét tứ giác AEDB có:
\(\widehat{AED}+\widehat{EDB}+\widehat{ABD}+\widehat{BAE}=360^0\)
\(\Rightarrow\widehat{EDB}=360^0-\widehat{AED}-\widehat{ABD}-\widehat{BAE}=360^0-90^0-40^0-60^0=170^0\)
\(\Rightarrow x=170^0\)
NM
giải gấp giúp mình vs, mình cảm ơn
1
VD
4
VP
5
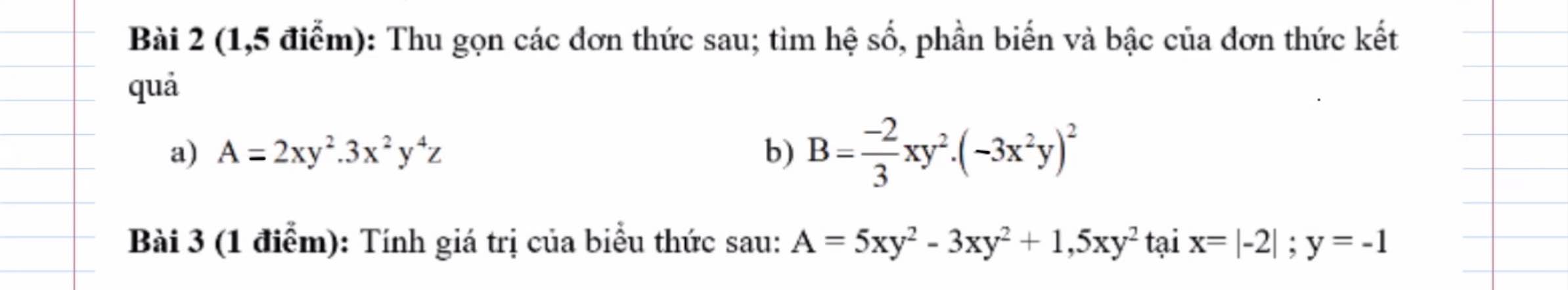
\(25\times\left(-\frac{1}{3}\right)^3+\frac{1}{5}-2\times\left(-\frac{1}{2}\right)^2-\left|-\frac{1}{2}\right|.\)
\(=25\times\left(-\frac{1}{27}\right)+\frac{1}{5}-2\times\frac{1}{4}-\frac{1}{2}\)
\(=-\frac{25}{27}+\frac{1}{5}-\frac{1}{2}-\frac{1}{2}\)
\(=-\frac{98}{135}-\frac{1}{2}-\frac{1}{2}\)
\(=-\frac{331}{270}-\frac{1}{2}==-\frac{233}{135}\)
cảm ơn bạn vì đã giúp tôi