K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LN
2
14 tháng 10 2021
Bài 9:
a: \(2^{195}=8^{65}\)
\(3^{130}=9^{65}\)
mà 8<9
nên \(2^{195}< 3^{130}\)
NT
1
8 tháng 3 2022
Câu 4:
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
Suy ra: BA=BH và EA=EH
b: Xét ΔAEK vuông tại A và ΔHEC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔAEK=ΔHEC
Suy ra: AK=HC
Ta có: BA+AK=BK
BH+HC=BC
mà BA=BH
và AK=HC
nên BK=BC
hay ΔBKC cân tại B
c: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
24 tháng 1 2022
Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 8: C
24 tháng 1 2022
Câu 1 : A
Câu 2 : B
Câu 3 : D
Câu 4 : A
Câu 5 : C
Câu 6 : B
Câu 7 : A
Câu 8 : C
HT
NT
4
VH
1
LM
Lê Minh Vũ
CTVHS
14 tháng 6 2023
\(2.16\ge2^n>4\)
\(2.2^4\ge2^n>2^2\)
\(2^5\ge2^n>2^2\)
=> \(n\in\left\{3,4,5\right\}\)
Vậy: \(n\in\left\{3,4,5\right\}\)
NT
2
7 tháng 3 2022
\(a.Thayx=-3:A=\left(-3\right)^2-2.\left(-3\right)+3.\\ =9+6+3=18.\)
\(b.Thay\) \(x=m;A=3:\)
\(3=m^2-2m+3.\\ \Leftrightarrow m^2-2m=0.\\ \Leftrightarrow\left[{}\begin{matrix}m=0.\\m=2.\end{matrix}\right.\)
NA
7 tháng 3 2022
Bài 1:
a, Biểu thức tính quãng đường đi được trong a giờ đầu tiên là: 40a
Biểu thức tính quãng đường AB là: 40a+50b
Bài 2:
a, Thay x=-3 vào A ta có:
\(A=x^2-2x+3=\left(-3\right)^2-2\left(-3\right)+3=9+6+3=18\)
b, Thay x=m, A=3 ta có:
\(m^2-2m+3=3\\ \Leftrightarrow m^2-2m=0\\ \Leftrightarrow m\left(m-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)
NT
1
7 tháng 3 2022
a) Xét \(\Delta ABC\) cân tại A:
AH là đường cao (gt).
\(\Rightarrow\) AH là đường phân giác \(\widehat{BAC}\) (T/c tam giác cân).
\(\Rightarrow\widehat{BAH}=\widehat{CAH}.\)
b) Xét \(\Delta ABC\) cân tại A:
AH là đường cao (gt).
\(\Rightarrow\) AH là đường trung tuyến (T/c tam giác cân).
\(\Rightarrow\) H là trung điểm của BC.
Xét \(\Delta ABC:\)
H là trung điểm của BC (cmt).
\(HI//AB\left(gt\right).\)
\(\Rightarrow\) I là trung điểm của AC.
Xét \(\Delta ABC:\)
I là trung điểm của AC (cmt).
H là trung điểm của BC (cmt).
\(\Rightarrow\) IH là đường trung bình.
\(\Rightarrow\) \(IH=\dfrac{1}{2}AB\) (T/c đường trung bình).
Mà \(AB=AC(\Delta ABC\) cân tại A\().\)
\(IC=\dfrac{1}{2}AC\) (I là trung điểm của AC).
\(\Rightarrow IH=IC.\)
\(\Rightarrow\Delta IHC\) cân tại I.
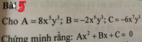
Bài 2:
a: Xét ΔACE vuông tại C và ΔAKE vuông tại K có
AE chung
\(\widehat{CAE}=\widehat{KAE}\)
Do đó: ΔACE=ΔAKE
=>AC=AK và EC=EK
Ta có: AC=AK
=>A nằm trên đường trung trực của CK(1)
Ta có: EC=EK
=>E nằm trên đường trung trực của CK(2)
Từ (1) và (2) suy ra AElà đường trung trực của CK
b: Ta có: ΔABC vuông tại C
=>\(\widehat{CAB}+\widehat{CBA}=90^0\)
=>\(\widehat{CBA}=90^0-60^0=30^0\)
AE là phân giác của góc CAB
=>\(\widehat{CAE}=\widehat{BAE}=\dfrac{\widehat{CAB}}{2}=30^0\)
Xét ΔEAB có \(\widehat{EAB}=\widehat{EBA}\)
nên ΔEAB cân tại E
Ta có: ΔEAB cân tại E
mà EK là đường cao
nên K là trung điểm của AB
c: Ta có: EB=EA
EA>AC(ΔEAC vuông tại C)
Do đó: EB>AC
bài 1:
a: FE là đường trung trực của AB
E\(\in\)AB
=>E là trung điểm của AB và FA=FB và FE\(\perp\)AB
b: ta có: FE\(\perp\)AB
AC\(\perp\)AB
Do đó: FE//AC
Ta có: FE//AC
FH\(\perp\)AC
Do đó: FH\(\perp\)FE
c: Xét tứ giác AEFH có
\(\widehat{AEF}=\widehat{FHA}=\widehat{HAE}=90^0\)
=>AEFH là hình chữ nhật
=>FH=AE
d: Ta có: \(\widehat{FAB}+\widehat{FAC}=\widehat{BAC}=90^0\)
\(\widehat{FBA}+\widehat{FCA}=90^0\)(ΔABC vuông tại A)
mà \(\widehat{FAB}=\widehat{FBA}\)(FA=FB)
nên \(\widehat{FAC}=\widehat{FCA}\)
=>FA=FC
mà FA=FB
nên FC=FB
=>F là trung điểm của BC
Xét ΔABC có
F là trung điểm của BC
FH//AB
Do đó: H là trung điểm của AC
Xét ΔABC có
E,H lần lượt là trung điểm của AB,AC
=>EH là đường trung bình của ΔABC
=>EH//BC và \(EH=\dfrac{BC}{2}\)