Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xin lỗi nha, mình ko biết vẽ hình trên máy nên bạn tự vẽ hình giùm mình nha
b)Ta có:\(\widehat{MNB}=\dfrac{1}{2}\stackrel\frown{BM}\left(1\right)\)( góc nội tiếp chắn cung BM)
\(\widehat{AEB}=\dfrac{1}{2}\left(\stackrel\frown{AB-\stackrel\frown{AM}}\right)\)= \(\dfrac{1}{2}\stackrel\frown{BM}\)(2) (Góc có đỉnh ngoài đường tròn)
Từ (1) và (2) ⇒ \(\widehat{MNB}=\widehat{AEB}\)
Xét Δ BMN và Δ BFE có:
\(\widehat{B}\): góc chung
\(\widehat{MNB}=\widehat{AEB}\) ( cùng chắn \(\stackrel\frown{BM}\) )
Do đó: Δ BMN \(\sim\) Δ BFE(g-g)
⇔ BM . BE =BN . BF (đpcm)
vẽ giùm cái hình đi, lười vẽ hình trên này quá

Hướng dẫn làm bài:
a) Giải phương trình: x2 – x – 2 = 0
∆ = (-1)2 – 4.1.(-2) = 1 + 8 > 0
√∆ = √9 = 3
⇒ x1 = -1; x2 = 2
b) Vẽ đồ thị hàm số
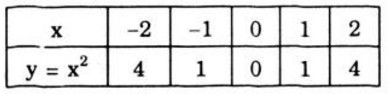
- Hàm số y = x2
+ Bảng giá trị:
- Hàm số y = x + 2
+ Cho x = 0 ⇒ y = 2 được điểm A(0,2)
+ Cho x = -2 ⇒ y = 0 được điểm B(-2;0)
Đồ thị hàm số:

c) Ta có phương trình hoành độ giao điểm của hai đồ thị là:
x2=x+2⇔x2−x−2=0⇔{x1=−1x2=2x2=x+2⇔x2−x−2=0⇔{x1=−1x2=2
Điều này chứng tỏ rằng đồ thị đường thẳng cắt đồ thị parapol tại hai điểm có hoành độ lần lượt là x = -1; x= 2. Hai giá trị này cũng chính là nghiệm của phương trình x2 - x - 2 = 0 ở câu a).


Xét phương trình hoàng độ giao điểm
-x+2= x2
=> x2 + x -2=0
=> x=1 => y= x2=1
x=-2 => y= 4
vậy :.....

Bài 1: b) Ptrình hoành độ giao điểm:
\(2x^2-4x=0\Leftrightarrow2x\left(x-2\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=0\\y=8\end{matrix}\right.\)
Vậy hai đồ thị giao tại (0;0);(2;8).
Bài 1:
a) Hình vẽ:

b) Gọi $(x_0,y_0)$ là giao điểm của 2 đồ thị. Khi đó:
\(\left\{\begin{matrix} y_0=2x_0^2\\ y_0=4x_0\end{matrix}\right.\Rightarrow 2x_0^2=4x_0\)
\(\Leftrightarrow 2x_0^2-4x_0=0\Leftrightarrow 2x_0(x_0-2)=0\Rightarrow x_0=0\) hoặc \(x_0=2\)
Với \(x_0=0\Rightarrow y_0=4x_0=0\). Ta có giao điểm $(0,0)$
Với \(x_0=2\Rightarrow y_0=4x_0=8\). Ta có giao điểm $(2,8)$

