
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a: Xét ΔDHE vuông tại H có HI là đường cao ứng với cạnh huyền DE
nên \(DI\cdot DE=DH^2\left(1\right)\)
Xét ΔDHF vuông tại H có HK là đường cao ứng với cạnh huyền DF
nên \(DK\cdot DF=DH^2\left(2\right)\)
Từ (1) và (2) suy ra \(DI\cdot DE=DK\cdot DF\)
Bài 2:
a: Xét ΔMKN vuông tại K có KE là đường cao ứng với cạnh huyền MN
nên \(ME\cdot MN=MK^2\left(1\right)\)
Xét ΔMKP vuông tại K có KF là đường cao ứng với cạnh huyền MP
nên \(MF\cdot MP=MK^2\left(2\right)\)
từ (1) và (2) suy ra \(ME\cdot MN=MF\cdot MP\)

bạn tự vẽ hình giúp mik nha
a. xét \(\Delta ADN\) và \(\Delta BAM\) có
AB=AD(gt)
\(\widehat{ADN}=\widehat{BAM}=90^o\)
DN=MA(N,M là trung điểm của cạnh DC,AD)
\(\Rightarrow\Delta ADN\sim\Delta BAM\left(c.g.c\right)\)
\(\Rightarrow\widehat{DNA}=\widehat{AMB}\)
mà:\(\widehat{DNA}+\widehat{DAN}=90^o\Rightarrow\widehat{BMA}+\widehat{DAN}=90^o\)
\(\Rightarrow\Delta MAI\) vuông tại I
\(\Rightarrow AI\perp MI\) hay \(MB\perp AN\)
b.ta có M là trung điểm của AD\(\Rightarrow AM=\dfrac{1}{2}AD=\sqrt{5}\)
trong \(\Delta MAB\) vuông tại A có
\(MB=\sqrt{AM^2+AB^2}=\sqrt{\sqrt{5^2}+\left(2\sqrt{5}\right)^2}=5\)
\(AM^2=MB.MI\Rightarrow MI=\dfrac{AM^2}{MB}=\dfrac{\sqrt{5^2}}{5^5}=0,2\)
\(AI.MB=AM.AB\Rightarrow AI=\dfrac{AM.AB}{MB}=\dfrac{\sqrt{5}.2\sqrt{5}}{5}\)=2
c.IB=MB-MI=5-0,2=4,8
\(S_{\Delta AIB}=\dfrac{AI.IB}{2}=\)\(\dfrac{2.4,8}{2}=4,8\)
\(S_{\Delta ADN}=\dfrac{AD.DN}{2}=\dfrac{2\sqrt{5}.\sqrt{5}}{2}=5\)
\(S_{\Delta ABCD}=\left(2\sqrt{5}\right)^2=20\)
\(S_{BINC}=S_{ABCD}-S_{\Delta AIB}-S_{\Delta DAN}\)=20-4,8-5=10,2

d.
Ta có: \(AB=AC\) (t/c hai tiếp tuyến cắt nhau)
\(OB=OC=R\)
\(\Rightarrow OA\) là trung trực BC hay OA vuông góc BC tại I
Xét hai tam giác vuông AIB và ABO có:
\(\left\{{}\begin{matrix}\widehat{AIB}=\widehat{ABO}=90^0\\\widehat{BAI}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta AIB\sim\Delta ABO\left(g.g\right)\)
\(\Rightarrow\dfrac{AI}{AB}=\dfrac{AB}{AO}\Rightarrow AI.AO=AB^2\)
Theo c/m câu c có \(AB^2=AE.AF\)
\(\Rightarrow AI.AO=AE.AF\)
e.
Từ đẳng thức trên ta suy ra: \(\dfrac{AI}{AF}=\dfrac{AE}{AO}\)
Xét hai tam giác AIE và AFO có:
\(\left\{{}\begin{matrix}\dfrac{AI}{AF}=\dfrac{AE}{AO}\left(cmt\right)\\\widehat{OAF}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta AIE\sim\Delta AFO\left(c.g.c\right)\)
\(\Rightarrow\widehat{AFO}=\widehat{AIE}\)
Mà \(\widehat{AIE}+\widehat{OIE}=180^0\) (kề bù)
\(\Rightarrow\widehat{AFO}+\widehat{OIE}=180^0\)
\(\Rightarrow\) Tứ giác FOIE nội tiếp
a.
Do AB là tiếp tuyến của (O) \(\Rightarrow AB\perp OB\Rightarrow\widehat{ABO}=90^0\)
\(\Rightarrow\) 3 điểm A, B, O thuộc đường tròn đường kính OA (1)
Tương tự AC là tiếp tuyến của (O) nên 3 điểm A, C, O thuộc đường tròn đường kính OA
\(\Rightarrow\) 4 điểm A, B, C, O thuộc đường tròn đường kính OA hay tứ giác ABOC nội tiếp
b.
Do M là trung điểm EF \(\Rightarrow OM\perp EF\Rightarrow\widehat{OMA}=90^0\)
\(\Rightarrow\) 3 điểm A, M, O thuộc đường tròn đường kính OA (2)
(1);(2) \(\Rightarrow\) 4 điểm A, B, M, O thuộc đường tròn đường kính OA
Hay tứ giác ABMO nội tiếp
c.
Xét hai tam giác ABE và AFB có:
\(\left\{{}\begin{matrix}\widehat{EAB}\text{ chung}\\\widehat{ABE}=\widehat{AFB}\left(\text{cùng chắn BE}\right)\end{matrix}\right.\) \(\Rightarrow\Delta ABE\sim\Delta AFB\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AF}=\dfrac{AE}{AB}\) \(\Rightarrow AB^2=AE.AF\)

\(a)\)\(\sqrt{15-6\sqrt{6}}+\sqrt{33-12\sqrt{6}}\)
\(=\)\(\sqrt{6-6\sqrt{6}+9}+\sqrt{24-12\sqrt{6}+9}\)
\(=\)\(\sqrt{\left(\sqrt{6}+3\right)}+\sqrt{\left(\sqrt{24}+3\right)}\)
\(=\)\(\left|\sqrt{6}+3\right|+\left|\sqrt{24}+3\right|\)
\(=\)\(\sqrt{6}+3+\sqrt{24}+3\)
\(=\)\(\sqrt{6}\left(1+\sqrt{4}\right)+9\)
\(=\)\(3\sqrt{6}+9\)
Chúc bạn học tốt ~
\(b)\)\(\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{4-2\sqrt{3}}\)
\(=\)\(\left|2-\sqrt{3}\right|+\sqrt{3-2\sqrt{3}+1}\)
\(=\)\(2-\sqrt{3}+\sqrt{\left(\sqrt{3}-1\right)^2}\) ( vì \(2=\sqrt{4}>\sqrt{3}\) )
\(=\)\(2-\sqrt{3}+\left|\sqrt{3}-1\right|\)
\(=\)\(2-\sqrt{3}+\sqrt{3}-1\) ( vì \(\sqrt{3}>\sqrt{1}=1\) )
\(=\)\(1\)
Chúc bạn học tốt ~
PS : mới lớp 8 sai thì thông cảm >.<

1:
=>|2x+5|=5
=>2x+5=5 hoặc 2x+5=-5
=>x=0 hoặc x=-5
2: =>|x-2|=3
=>x-2=3 hoặc x-2=-3
=>x=-1 hoặc x=5
3: =>|2x-1|=1
=>2x-1=1 hoặc 2x-1=-1
=>x=0 hoặc x=1

Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)






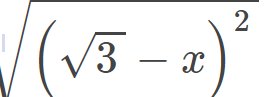
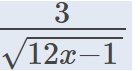 GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
a) Xét (O) có
\(\widehat{PFE}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{PFE}=90^0\)(Hệ quả góc nội tiếp)
hay \(\widehat{PFN}=90^0\)
Xét tứ giác PFMN có
\(\widehat{PFN}\) và \(\widehat{PMN}\) là hai góc cùng nhìn cạnh PN
\(\widehat{PFN}=\widehat{PMN}\left(=90^0\right)\)
Do đó: PFMN là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)