K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LO
1
30 tháng 12 2021
Câu 3:
b: Tọa độ giao điểm là;
\(\left\{{}\begin{matrix}-3x+3=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{3}{2}\end{matrix}\right.\)
S2
1
20 tháng 5 2022
\(\text{Δ}=\left(-3\right)^2-4\cdot\left(2m+1\right)\)
=9-8m-4=-8m+5
Để phương trình có nghiệm kép thì -8m+5=0
hay m=5/8
Pt trở thành \(x^2-3x+\dfrac{9}{4}=0\)
hay x=3/2
PM
1
11 tháng 5 2022
Bài 1:
Vì (d)//y=-2x+1 nên a=-2
Vậy: y=-2x+b
Thay x=1 và y=2 vào (d),ta được:
b-2=2
hay b=4
17 tháng 8 2021
Em tách ra 1-2 bài/1 câu hỏi để mọi người hỗ trợ nhanh nhất nha!
20 tháng 5 2021
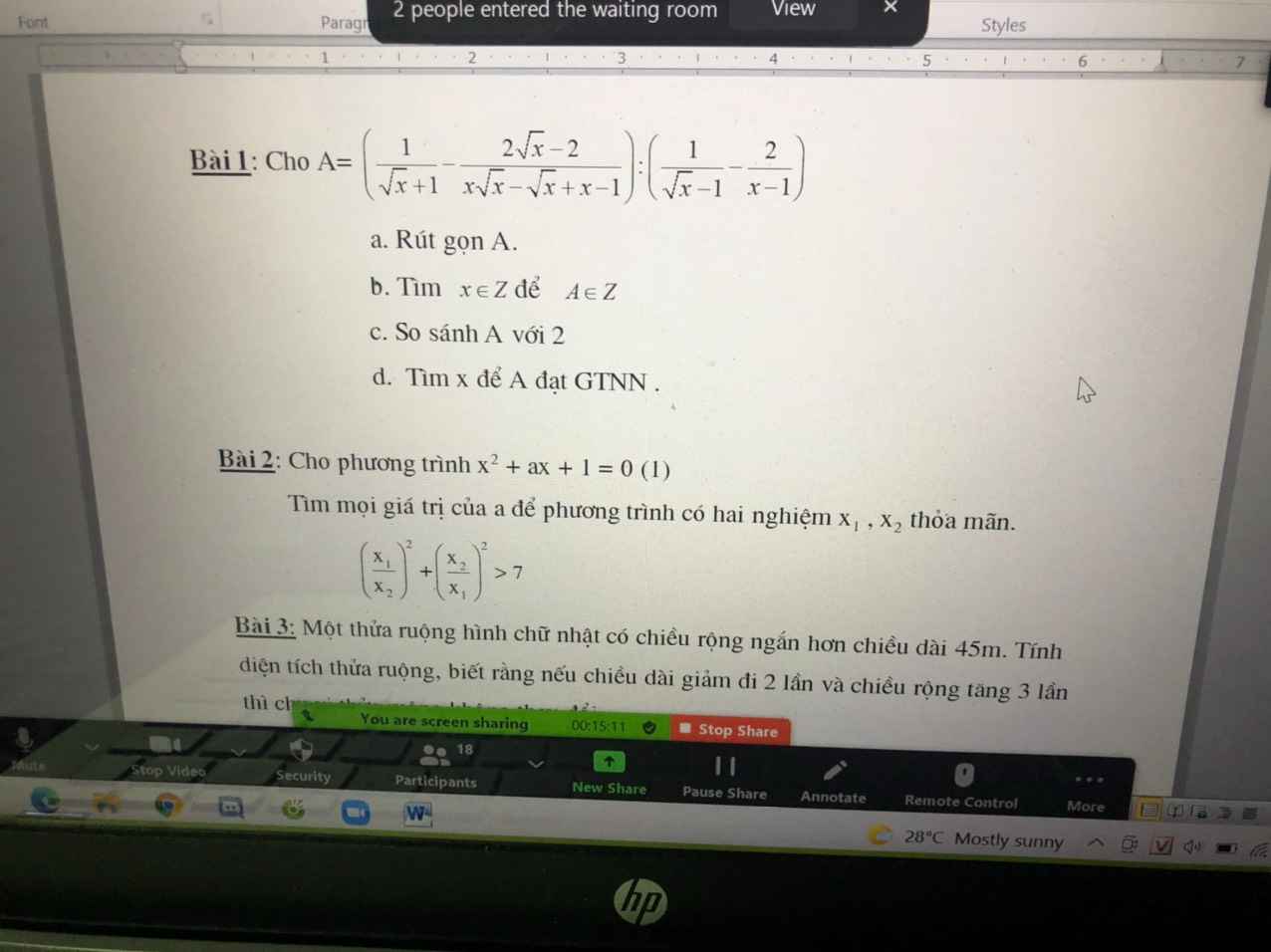
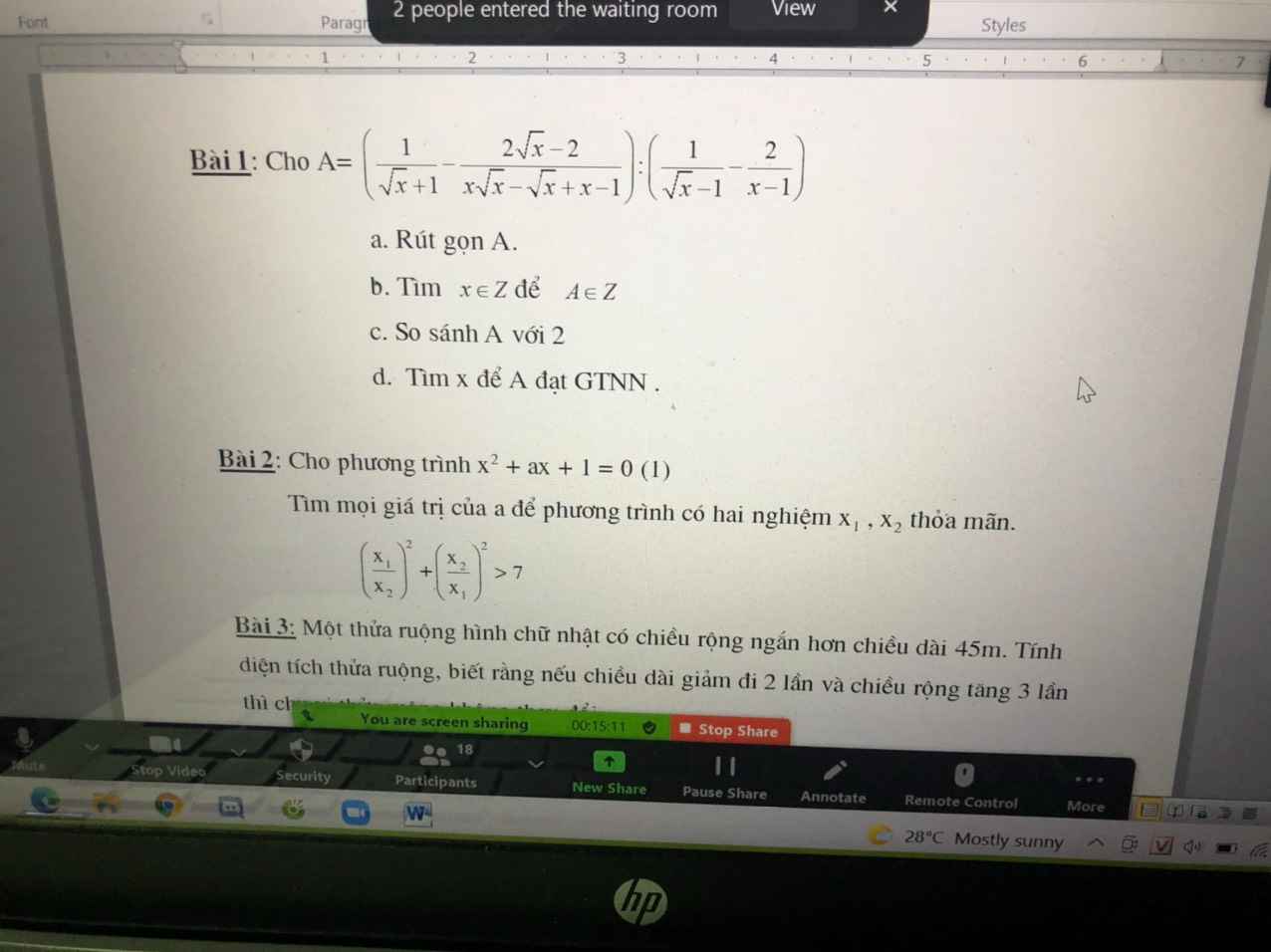
A=\(\left(\dfrac{1}{\sqrt{x}+1}-\dfrac{2\sqrt{x}-2}{x\sqrt{x}-\sqrt{x}+x-1}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2}{x-1}\right)\) (đk: \(x\ge0;x\ne1\))
\(=\left[\dfrac{1}{\sqrt{x}+1}-\dfrac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(x-1\right)}\right]:\dfrac{\sqrt{x}+1-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\left[\dfrac{1}{\sqrt{x}+1}-\dfrac{2}{\left(\sqrt{x}+1\right)^2}\right]:\dfrac{1}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}+1-2}{\left(\sqrt{x}+1\right)^2}.\left(\sqrt{x}+1\right)=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
b, \(A=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=1-\dfrac{2}{\sqrt{x}+1}\)
Để \(A\in Z\Leftrightarrow\dfrac{2}{\sqrt{x}+1}\in Z\) mà với mọi \(x\in Z\),\(x\ge0\) thì \(\left\{{}\begin{matrix}\dfrac{2}{\sqrt{x}+1}>0\\\dfrac{2}{\sqrt{x}+1}\le\dfrac{2}{\sqrt{0}+1}=2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{2}{\sqrt{x}+1}=1\\\dfrac{2}{\sqrt{x}+1}=2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(L\right)\\x=0\left(TM\right)\end{matrix}\right.\)
Vậy x=0 thì A=-1
c, Vì \(\dfrac{2}{\sqrt{x}+1}>0\Rightarrow\) \(A=1-\dfrac{2}{\sqrt{x}+1}< 1< 2\)
Vậy A<2
d, \(\sqrt{x}\ge0\Rightarrow\sqrt{x}+1\ge1\Leftrightarrow\dfrac{2}{\sqrt{x}+1}\le2\)
\(\Rightarrow1-\dfrac{2}{\sqrt{x}+1}\ge1-2\)
Hay \(A\ge-1\)
Dấu = xảy ra khi x=0
4 tháng 1 2022
\(7,\\ a,ĐK:a>0;a\ne1\\ b,K=\dfrac{a-1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{\sqrt{a}-1+2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\\ K=\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}=\dfrac{a-1}{\sqrt{a}}\\ c,a=3+2\sqrt{2}=\left(\sqrt{2}+1\right)^2\\ \Leftrightarrow K=\dfrac{3+2\sqrt{2}-1}{\sqrt{2}+1}=\dfrac{2+2\sqrt{2}}{\sqrt{2}+1}=\dfrac{2\left(\sqrt{2}+1\right)}{\sqrt{2}+1}=2\\ d,K< 0\Leftrightarrow a-1< 0\left(\sqrt{a}>0\right)\Leftrightarrow0< a< 1\)
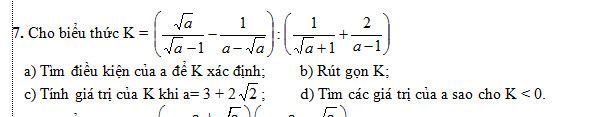
Bài 3:
a: Xét ΔOAM vuông tại A và ΔOBP vuông tại B có
OA=OB
góc AOM=góc BOP
Do đó: ΔOAM=ΔOBP
=>OM=OP
Xét ΔNMP có
NO vừa là đường cao, vừa là trung tuyến
nên ΔMNP cân tại N
=>NM=NP
b: góc NMP=góc NPM
=>góc NMP=góc AMO
Xét ΔMAO vuông tại A và ΔMIO vuông tại I có
MO chung
góc AMO=góc IMO
=>ΔMAO=ΔMIO
=>OI=OA=R
=>MN là tiếp tuyên của (O)