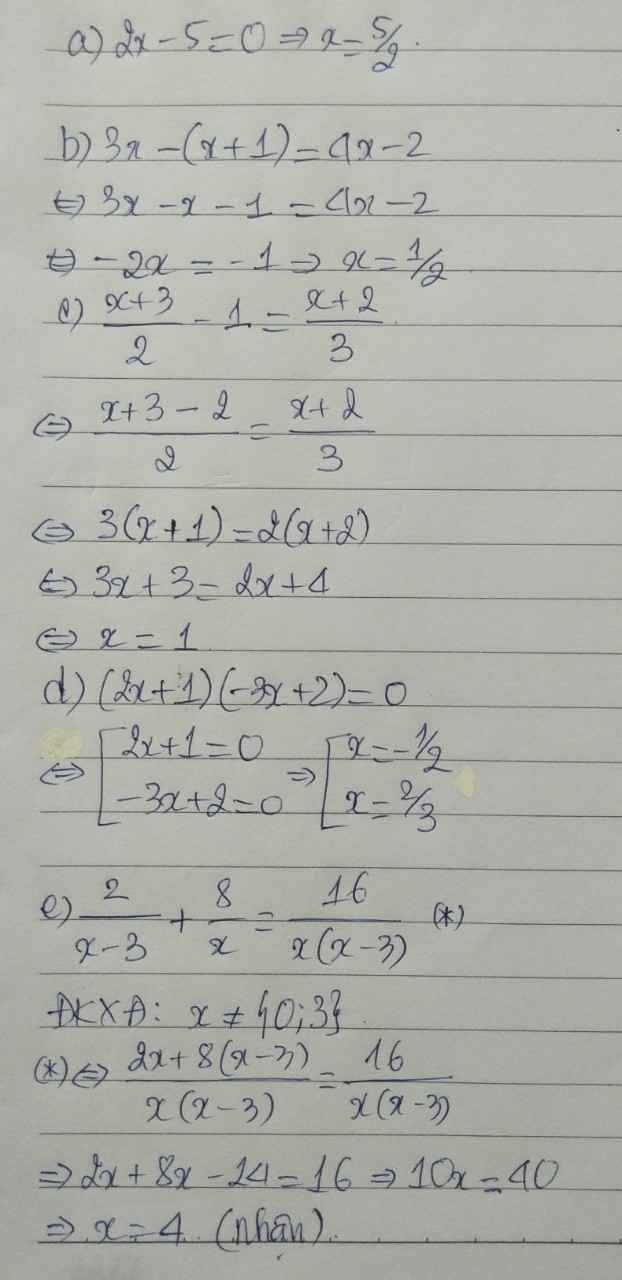K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 8 2021
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
NH
0
26 tháng 9 2021
1: Ta có: \(a^2+2ab+b^2-12a-12b+50\)
\(=\left(a+b\right)^2-12\left(a+b\right)+50\)
\(=2^2-12\cdot2+50\)
=54-24
=30
22 tháng 3 2022
a, \(2x=5\Leftrightarrow x=\dfrac{5}{2}\)
b, \(2x-1=4x-8\Leftrightarrow2x=7\Leftrightarrow x=\dfrac{7}{2}\)
c, \(3x+9-6=2x+4\Leftrightarrow x=1\)
d, \(\left[{}\begin{matrix}2x+1=0\\-3x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=\dfrac{2}{3}\end{matrix}\right.\)
e, đk : x khác 0 ; 3
\(2x+8x-24=16\Leftrightarrow10x=40\Leftrightarrow x=4\left(tm\right)\)
31 tháng 10 2021
3: \(\left(3x+5\right)\left(2x-7\right)\)
\(=6x^2-21x+10x-35\)
\(=6x^2-11x-35\)
4: \(\left(5x-2\right)\left(3x+4\right)\)
\(=15x^2+20x-6x-8\)
\(=15x^2+14x-8\)
NH
13 tháng 12 2022
\(\left(x^3-8\right):\left(x^2+2x+4\right)\\ =\left(x-2\right)\left(x^2+2x+4\right):\left(x^2+2x+4\right)\\ =x-2\)
bài 2
a)
\(2xy^2-4y\\ =2y\left(xy-2\right)\)
b)
\(x^2-6xy+9y^2\\ =\left(x-3y\right)^2\)
c)
\(x^2+x-y^2+y\\ =\left(x^2-y^2\right)+\left(x+y\right)\\ =\left(x-y\right)\left(x+y\right)+\left(x+y\right)\\ =\left(x+y\right)\left(x-y+1\right)\)
d)
\(x^2+4x+3\\ =x^2+3x+x+3\\ =x\left(x+3\right)+\left(x+3\right)\\ =\left(x+3\right)\left(x+1\right)\)
KV
25 tháng 9 2023
Bài 16
a) x² + 2x + 2
= x² + 2x + 1 + 1
= (x + 1)² + 1
Do (x + 1)² ≥ 0 với mọi x ∈ R
⇒ (x + 1)² + 1 > 0 với mọi x ∈ R
b) 9a² - 6a + 3
= 9a² - 6a + 1 + 2
= (3a - 1)² + 2
Do (3a - 1)² ≥ 0 với mọi a ∈ R
⇒ (3a - 1)² + 2 > 0 với mọi a ∈ R
KV
25 tháng 9 2023
Bài 17
M = y² + 6y + 7
= y² + 6y + 9 - 2
= (y + 3)² - 2
(y + 3)² ≥ 0 với mọi y ∈ R
⇒ (y + 3)² - 2 ≥ -2 với mọi y ∈ R
Vậy GTNN của M là -2 khi y = -3
------------
H = 16b² - 16b + 5
= 16b² - 16 + 4 + 1
= (4b - 2)² + 1
Do (4b - 2)² ≥ 0 với mọi b ∈ R
⇒ (4b - 2)² + 1 ≥ 1 với mọi b ∈ R
Vậy GTNN của H là 1 khi b = 1/2
------------
T = x² + y² + 2x + 1 - 2y
= x² + 2x + 1 + y² - 2y + 1 - 1
= (x + 1)² + (y - 1)² - 1
Do (x + 1)² ≥ 0 với mọi x ∈ R
(y - 1)² ≥ 0 với mọi y ∈ R
⇒ (x + 1)² + (y - 1)² ≥ 0 với mọi x, y ∈ R
⇒ (x + 1)² + (y - 1)² - 1 ≥ -1 với mọi x, y ∈ R
Vậy GTNN của T là -1 khi x = -1; y = 1
2 tháng 9 2021
Bài 8:
a: Ta có: \(A=\left(\dfrac{x-2}{x^2-1}-\dfrac{x+2}{x^2+2x+1}\right)\cdot\dfrac{x^4-2x^2+1}{2}\)
\(=\dfrac{\left(x-2\right)\left(x+1\right)-\left(x+2\right)\left(x-1\right)}{\left(x+1\right)^2\cdot\left(x-1\right)}\cdot\dfrac{\left(x-1\right)^2\cdot\left(x+1\right)^2}{2}\)
\(=\dfrac{x^2-x-2-x^2-x-2}{1}\cdot\dfrac{x-1}{2}\)
\(=\dfrac{-2x\cdot\left(x-1\right)}{2}=-x\left(x-1\right)\)
2 tháng 9 2021
Bài 8:
a) \(A=\left(\dfrac{x-2}{x^2-1}-\dfrac{x+2}{x^2+2x+1}\right).\dfrac{x^4-2x^2+1}{2}\left(đk:x\ne1,x\ne-1\right)\)
\(=\dfrac{\left(x-2\right)\left(x+1\right)-\left(x+2\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)^2}.\dfrac{\left(x^2-1\right)^2}{2}=\dfrac{x^2-x-2-x^2-x+2}{\left(x-1\right)\left(x+1\right)^2}.\dfrac{\left(x-1\right)^2\left(x+1\right)^2}{2}=\dfrac{-2x\left(x-1\right)}{2}=-x^2+x\)
b) \(x^2-3x+2=0\Leftrightarrow\left(x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)\(\Leftrightarrow x=2\)(do đkxđ của A là \(x\ne1\))
\(A=-x^2+x=-2^2+2=-2\)
c) Do \(A=-x^2+x\in Z\forall x\in Z\)
\(\Rightarrow A\in Z\Leftrightarrow x\in Z\)
28 tháng 12 2021
Bài 10:
e: \(\Leftrightarrow x\left(x+2\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)