
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ:\(x\ne\pm1\)
\(\dfrac{x-1}{x+1}-\dfrac{x+1}{x-1}=\dfrac{14}{x^2-1}\\ \Leftrightarrow\dfrac{\left(x-1\right)^2}{\left(x+1\right)\left(x-1\right)}-\dfrac{\left(x+1\right)^2}{\left(x+1\right)\left(x-1\right)}-\dfrac{14}{\left(x+1\right)\left(x-1\right)}=0\\ \Rightarrow x^2-2x+1-x^2-2x-1-14=0\\ \Leftrightarrow-4x-14=0\\ \Leftrightarrow x=-\dfrac{7}{2}\left(tm\right)\)

\(ĐK:x\ne0;2\)
\(\Leftrightarrow\dfrac{x+2}{x}-\dfrac{2x+3}{2\left(x-2\right)}=0\)
\(\Leftrightarrow\dfrac{2\left(x-2\right)\left(x+2\right)-x\left(2x+3\right)}{2x\left(x-2\right)}=0\)
\(\Leftrightarrow2\left(x^2-4\right)-x\left(2x+3\right)=0\)
\(\Leftrightarrow2x^2-8-2x^2-3x=0\)
\(\Leftrightarrow-3x=8\Leftrightarrow x=-\dfrac{8}{3}\left(tm\right)\)

\(a,=a^2+2a+1-a^2+2a-1-3a^2+3=-3a^2+4a+3\\ b,=\left[\left(m^3-m+1\right)-\left(m^2-3\right)\right]^2\\ =\left(m^3-m^2-m+4\right)^2\)

\(15x-9x^2-25+15x+9x^2+18x+9-30=0\)
\(48x-46=0\)
\(x=\dfrac{46}{48}=\dfrac{23}{24}\)
\(x^2+8x+16-x^2+1-16=0\)
\(8x+1=0\)
\(x=\dfrac{-1}{8}\)
a) \(\Leftrightarrow15x-9x^2-25+15x+9x^2+18x+9=30\)
\(\Leftrightarrow23x=46\)
\(\Leftrightarrow x=2\)
b) \(\Leftrightarrow x^2+8x+16-x^2+1=16\)
\(\Leftrightarrow x=-\dfrac{1}{8}\)


\(\left(1\right)8x-3=6x+11\)
\(\Leftrightarrow2x=14\)
\(\Leftrightarrow x=7\)
Vậy ...
\(\left(2\right)7-\left(2x+4\right)=-\left(x+4\right)\)
\(\Leftrightarrow7-2x-4=-x-4\)
\(\Leftrightarrow x=7\)
Vậy ...
\(\left(3\right)\dfrac{7x-1}{6}+2x=\dfrac{16-x}{5}\)
\(\Leftrightarrow5\left(7x-1\right)+60x=6\left(16-x\right)\)
\(\Leftrightarrow35x-5+60x=96-6x\)
\(\Leftrightarrow101x=101\)
\(\Leftrightarrow x=1\)
`1)8x-3=6x+11`
`<=>8x-6x=11+3`
`<=>2x=14`
`<=>x=7`
Vậy `S = {7}`
______________________________
`2)7-(2x+4)=-(x+4)`
`<=>7-2x-4=-x-4`
`<=>2x-x=7-4+4`
`<=>x=7`
Vậy `S = {7}`
______________________________
`3)[7x-1]/6+2x=[16-x]/5`
`<=>[5(7x-1)]/30+[60x]/30=[6(16-x)]/30`
`<=>35x-5+60x=96-6x`
`<=>35x+60x+6x=96+5`
`<=>101x=101`
`<=>x=1`
Vậy `S = {1}`

a: Xét ΔKNM vuông tại K và ΔMNP vuông tại M có
góc N chung
=>ΔKNM đồng dạng với ΔMNP
b: \(MP=\sqrt{PK\cdot PN}=10\left(cm\right)\)

Xét tam giác ABC và tam giác HBA, có:
^B: chung
^H=^A= 90 độ
Vậy tam giác ABC đồng dạng tam giác HBA ( g.g ) ( 1 )
\(\Rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
\(\Leftrightarrow AB^2=HB.BC\)
b.Xét tam giác ABC và tam giác HAC, có:
^C: chung
^A=^H = 90 độ
Vậy tam giác ABC đồng dạng tam giác HAC ( g.g ) ( 2 )
\(\Rightarrow\dfrac{AC}{HC}=\dfrac{BC}{AC}\)
\(\Leftrightarrow AC^2=HC.BC\)
c.Bạn check lại đề
c. Từ (1) và (2) Suy ra: Tam giác HBA đồng dạng tam giác HAC
\(\Rightarrow\dfrac{AH}{HC}=\dfrac{HB}{AH}\)
\(\Leftrightarrow AH^2=HB.HC\)


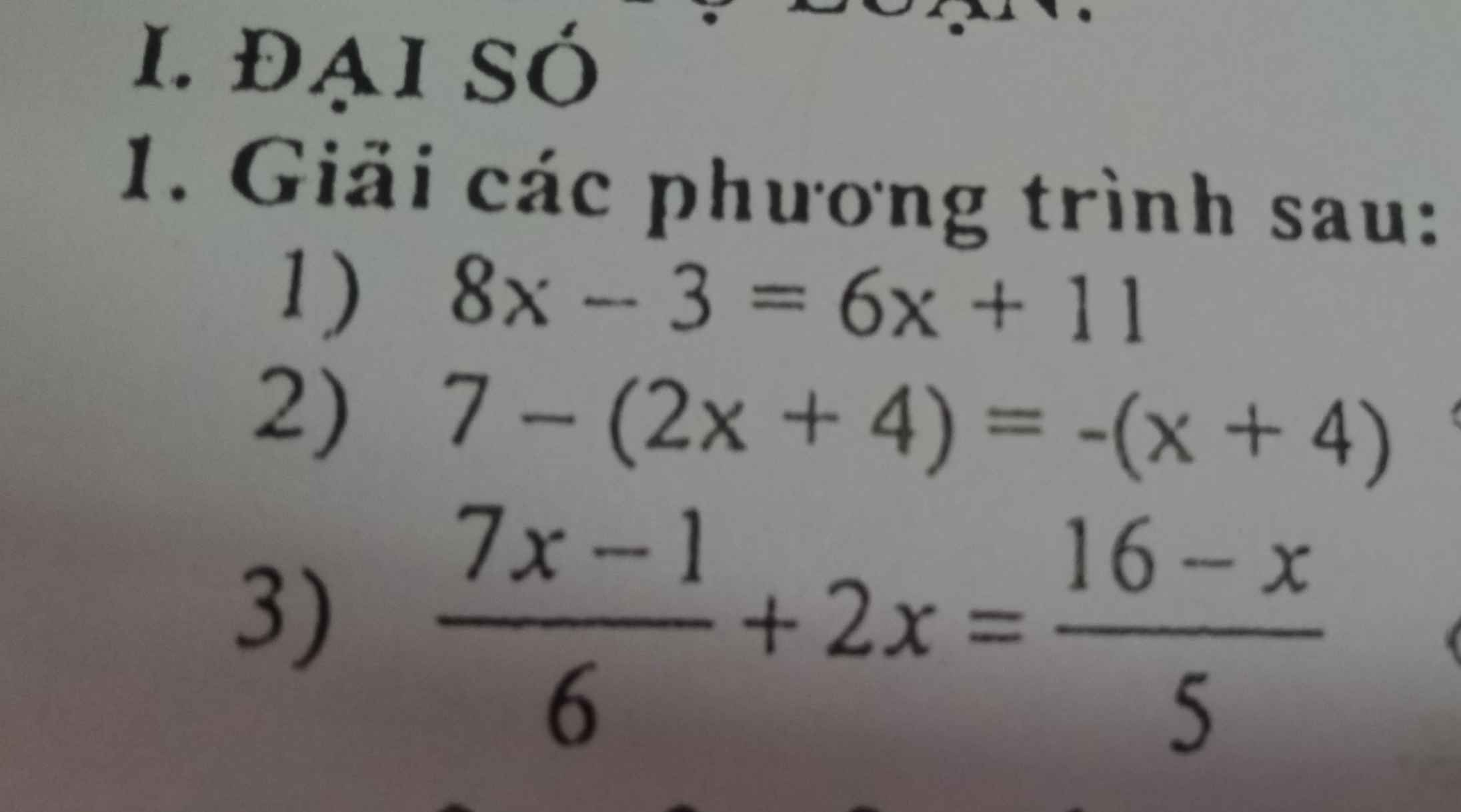


a. ĐKXĐ: \(2x^2-10x\ne0\Rightarrow x\ne\left\{0;5\right\}\)
b.
\(\dfrac{25x^2-5x^3}{2x^2-10x}=\dfrac{5x^2\left(5-x\right)}{-2x\left(5-x\right)}=-\dfrac{5}{2}x\)
Khi đó \(\dfrac{25x^2-5x^3}{2x^2-10x}=1\Rightarrow-\dfrac{5}{2}x=1\)
\(\Rightarrow x=-\dfrac{2}{5}\)
c.
Tại \(x=-10\Rightarrow-\dfrac{5}{2}.\left(-10\right)=25\)
Tại \(x=5\) phân thức đã cho không xác định (theo điều kiện đã tìm ở câu a)