K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 8 2021
Bài 10: A
Bài 11:
Áp dụng hệ thức về cạnh và góc trong tam giác vào tam giác vuông, ta được:
AC = AB.tan\(^{50^0}\) = 21.tan\(^{50^0}\) \(\approx\) 25
BC = \(\dfrac{AB}{\sin C}\)= \(\dfrac{21}{sin40^0}\)\(\approx\)33
BD = \(\dfrac{AB}{\cos25^0}\)=\(\dfrac{21}{\cos25^0}\)\(\approx\)23
25 tháng 6 2021
7)Đk \(x\le2\)
Pt \(\Leftrightarrow x^2-x+8=4-2x\)
\(\Leftrightarrow x^2+x+4=0\)
\(\Delta=-15< 0\) => vô nghiệm
Vậy pt vô nghiệm
10) \(\sqrt{9x+9}-4\sqrt{\dfrac{x+1}{4}}=5\) (đk: \(x\ge-1\)
\(\Leftrightarrow\sqrt{\left(x+1\right).9}-\dfrac{4\sqrt{x+1}}{\sqrt{4}}=5\)
\(\Leftrightarrow3\sqrt{x+1}-2\sqrt{x+1}=5\)
\(\Leftrightarrow\sqrt{x+1}=5\) \(\Leftrightarrow x=24\) (tm)
Vậy \(S=\left\{24\right\}\)
HN
5 tháng 4 2022
\(\dfrac{10+2\sqrt{10}}{\sqrt{5}+\sqrt{2}}+\dfrac{8}{1-\sqrt{5}}\) = \(\dfrac{2\sqrt{5}\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{5}+\sqrt{2}}+\dfrac{8}{-\dfrac{4}{1+\sqrt{5}}}\) = \(2\sqrt{5}-2\left(1+\sqrt{5}\right)\) = -2.
NT
1
3 tháng 8 2017
(x^2+6x+5)(x^2+6x+8)=10
Đặt x^2+6x+5=a>>>(a+3)a=10
a^2+3a-10=0 >>>(a+5)(a-2)=0>>>a=-5 hoặc a=2
Đến đây thay a =x^2+6x+5 ròi giải
24 tháng 8 2021
Bài 11:
a: Ta có: \(P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}\)
\(=\sqrt{x}\cdot\left(\sqrt{x}-1\right)\)
\(=x-\sqrt{x}\)
b: Để P=2 thì \(x-\sqrt{x}-2=0\)
hay x=4
24 tháng 8 2021
Bài 10:
a: Ta có: \(A=\left(1+\dfrac{\sqrt{x}}{x+1}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x\sqrt{x}+\sqrt{x}-x-1}\right)\)
\(=\dfrac{x+\sqrt{x}+1}{x+1}:\dfrac{x-2\sqrt{x}+1}{\left(x+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+\sqrt{x}+1}{x+1}\cdot\dfrac{x+1}{\sqrt{x}-1}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}-1}\)
b: Để A<0 thì \(\sqrt{x}-1< 0\)
hay x<1
Kết hợp ĐKXĐ, ta được: \(0\le x< 1\)
Để A=-1 thì \(x+\sqrt{x}+1=-\sqrt{x}+1\)
\(\Leftrightarrow x=0\)
c: Thay x=4 vào A, ta được:
\(A=\dfrac{4+2+1}{2-1}=7\)
10 tháng 10 2021
d: \(\dfrac{\sqrt{a+3}+\sqrt{a-3}}{\sqrt{a+3}-\sqrt{a-3}}\)
\(=\dfrac{a+3+a-3+2\sqrt{a^2-9}}{a+3-a+3}\)
\(=\dfrac{2a+2\sqrt{a^2-9}}{6}\)
\(=\dfrac{a+\sqrt{a^2-9}}{3}\)
16 tháng 4 2022
Theo hệ thức Vi-ét, ta có:\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{5}{2}\\x_1.x_2=\dfrac{1}{2}\end{matrix}\right.\)
\(x_1+x_2-3x_1x_2=-\dfrac{5}{2}-3.\dfrac{1}{2}=-\dfrac{5}{2}-\dfrac{3}{2}=\dfrac{-5-3}{2}=-\dfrac{8}{2}=-4\)
=> Chọn D
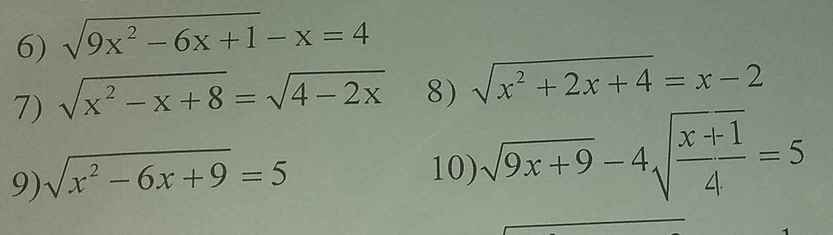
\(10,\\ a,=\dfrac{\sqrt{2}\left(1-\sqrt{2}+\sqrt{3}\right)}{1-\left(\sqrt{2}-\sqrt{3}\right)^2}=\dfrac{\sqrt{2}-2+\sqrt{6}}{1-5+2\sqrt{6}}=\dfrac{\sqrt{2}-2+\sqrt{6}}{2\sqrt{6}-4}\\ =\dfrac{1-\sqrt{2}+\sqrt{3}}{2\sqrt{3}-2\sqrt{2}}=\dfrac{\left(1-\sqrt{2}+\sqrt{3}\right)\left(2\sqrt{3}+2\sqrt{2}\right)}{4}\\ =\dfrac{2\sqrt{3}+2\sqrt{2}-2\sqrt{6}-4+6+2\sqrt{6}}{4}\\ =\dfrac{2\sqrt{3}+2\sqrt{2}+2}{4}=\dfrac{\sqrt{3}+\sqrt{2}+1}{4}\)
\(b,=\dfrac{1}{3\sqrt{2}+2\sqrt{2}-2\sqrt{2}}=\dfrac{1}{4\sqrt{2}}=\dfrac{\sqrt{2}}{8}\\ c,=\dfrac{\sqrt{3}-\sqrt{2}+\sqrt{5}}{3-\left(\sqrt{2}-\sqrt{5}\right)^2}=\dfrac{\sqrt{3}-\sqrt{2}+\sqrt{5}}{3-7+2\sqrt{10}}\\ =\dfrac{\sqrt{5}+\sqrt{3}-\sqrt{2}}{2\sqrt{10}-4}=\dfrac{\left(\sqrt{5}+\sqrt{3}-\sqrt{2}\right)\left(2\sqrt{10}+4\right)}{24}\\ =\dfrac{10\sqrt{2}+4\sqrt{5}+2\sqrt{30}+4\sqrt{3}-4\sqrt{5}-4\sqrt{2}}{24}\\ =\dfrac{6\sqrt{2}+2\sqrt{30}+4\sqrt{3}}{24}=\dfrac{3\sqrt{2}+\sqrt{30}+2\sqrt{3}}{12}\)
câu d a thịnh làm r nhé