
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Ta có:
\(\dfrac{AB}{DE}=\dfrac{3}{15}=\dfrac{1}{5}\)
\(\dfrac{AC}{DF}=\dfrac{4}{20}=\dfrac{1}{5}\)
\(\dfrac{BC}{EF}=\dfrac{5}{25}=\dfrac{1}{5}\)
\(\Rightarrow\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{EF}=\dfrac{1}{5}\)
Xét hai tam giác ABC và DEF có:
\(\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{EF}\left(=\dfrac{1}{5}\right)\)
\(\Rightarrow\Delta ABC\sim\Delta DEF\left(c.c.c\right)\)

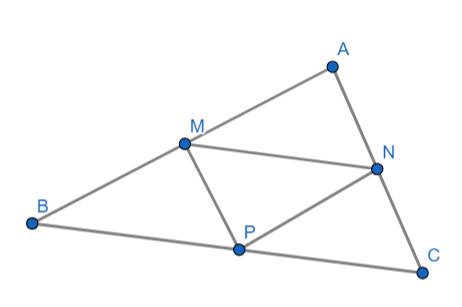
a) Ta có:
M là trung điểm của AB
N là trung điểm của AC
⇒ MN là đường trung bình của tam giác ABC
⇒ MN // BC
\(\Rightarrow\widehat{AMN}=\widehat{ABC}\) (đồng vị)
Xét hai tam giác ABC và AMN có:
\(\widehat{AMN}=\widehat{ABC}\left(cmt\right)\)
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta ABC\sim\Delta AMN\left(g.g\right)\)
b) Chứng minh tương tự như câu a thì ta có:
PN cũng là đường trung bình của tam giác ABC \(\Rightarrow PN=\dfrac{1}{2}AB\)
PM cũng là đường trung bình của tam giác ABC \(\Rightarrow PM=\dfrac{1}{2}AC\)
Mà: \(NM=\dfrac{1}{2}BC\) (NM là đường trung bình ...)
Xét hai tam giác ABC và PNM có:
\(\dfrac{PN}{AB}=\dfrac{PM}{AC}=\dfrac{NM}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\Delta ABC\sim\Delta PNM\left(c.c.c\right)\)

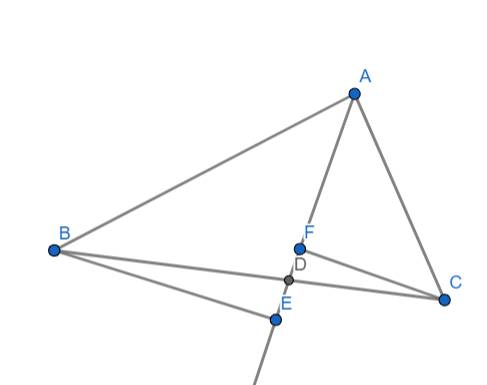
a) Ta có: E,F lần lược là hình chiếu của B,C trên AD
\(\Rightarrow\left\{{}\begin{matrix}\widehat{BEA}=90^o\\\widehat{CFA}=90^o\end{matrix}\right.\)
Xét hai tam giác ABE và ACF có:
\(\widehat{BEA}=\widehat{CFA}\left(=90^o\right)\)
\(\widehat{BAE}=\widehat{CAF}\) (do AD là phân giác của góc A)
\(\Rightarrow\Delta ABE\sim\Delta ACF\left(g.g\right)\)
b) Xét hai tam giác BDE và CDF có:
\(\widehat{BDE}=\widehat{CDF}\) (đối đỉnh)
\(\widehat{BED}=\widehat{CFD}\left(=90^o\right)\)
\(\Rightarrow\Delta BDE\sim\Delta CDF\left(g.g\right)\)
\(\Rightarrow\dfrac{BE}{CF}=\dfrac{DE}{DF}\) (1)
Mà: \(\Delta ABE\sim\Delta ACF\left(cmt\right)\)
\(\Rightarrow\dfrac{BE}{CF}=\dfrac{AE}{AF}\left(2\right)\)
Từ (1) và (2) ta có: \(\dfrac{DE}{DF}=\dfrac{AE}{AF}\Rightarrow AF\cdot DE=AE\cdot DF\)

a) Đường thẳng \(y=ax+b\) song song với đường thẳng \(y=4x-3\)
Nên có \(a=4\) đường thẳng có dạng \(y=3x+b\left(b\ne-3\right)\)
Mà \(y=3x+b\) đi qua điểm \(I\left(\dfrac{1}{2};\dfrac{3}{4}\right)\) nên ta thay \(x=\dfrac{1}{2};y=\dfrac{3}{4}\) ta có:
\(\dfrac{3}{4}=3\cdot\dfrac{1}{2}+b\)
\(\Leftrightarrow\dfrac{3}{4}=\dfrac{3}{2}+b\)
\(\Leftrightarrow b=\dfrac{3}{4}-\dfrac{3}{2}\)
\(\Leftrightarrow b=-\dfrac{3}{4}\left(tm\right)\)
Vậy: \(y=4x-\dfrac{3}{4}\)
b) Đường thẳng \(y=ax+b\) có hệ số góc \(a=3\) nên có dạng \(y=3x+b\)
Do đường thẳng cắt trục tung tại điểm có tung độ là - 4 nên ta thay \(x=0;y=-4\)
\(-4=0\cdot3+b\)
\(\Leftrightarrow b=-4\)
Vậy: \(y=3x-4\)

\(y=\left(m-3\right)+m^2\) có: \(\left\{{}\begin{matrix}a=m-3\\b=m^2\end{matrix}\right.\)
a) Để \(y=\left(m-3\right)x+m^2\) cắt \(y=3x+5\) thì:
\(a\ne a'\) hay:
\(m-3\ne3\)
\(\Leftrightarrow m\ne3+3\)
\(\Leftrightarrow m\ne6\)
b) Để \(y=\left(m-3\right)x+m^2\) song song với \(y=-2x+1\) thì
\(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\) hay:
\(\left\{{}\begin{matrix}m-3=-2\\m^2\ne1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=-2+3\\m\ne\pm1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m\ne\pm1\end{matrix}\right.\) (ktm)
Vậy không có m thỏa mãn
c) Để \(y=\left(m-3\right)x+m^2\) trùng với \(y=-x+4\) thì
\(\left\{{}\begin{matrix}a=a'\\b=b'\end{matrix}\right.\) hay:
\(\left\{{}\begin{matrix}m-3=-1\\m^2=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=-1+3\\m=\pm2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=2\\m=\pm2\end{matrix}\right.\Leftrightarrow m=2\)

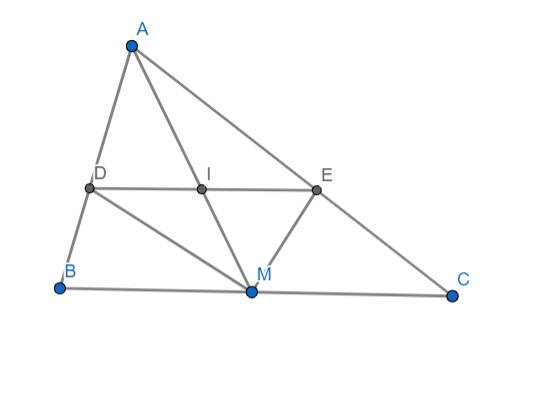
a) Ta có ME là tia phân giác của góc AMC nên:
\(\dfrac{AM}{AE}=\dfrac{MC}{CE}\Rightarrow\dfrac{AM}{MC}=\dfrac{AE}{CE}\) (1)
MD là tia phân giác của góc AMB nên:
\(\dfrac{AM}{AD}=\dfrac{BM}{BD}\Rightarrow\dfrac{AM}{BM}=\dfrac{AM}{CM}=\dfrac{AD}{BD}\) (vì M là trung điểm của BC nên BM = CM) (2)
Từ (1) và (2) ta có: \(\dfrac{AE}{CE}=\dfrac{AD}{BD}\Rightarrow DE//BC\)
b) Ta có: \(\Delta ADE\sim\Delta ABC\left(g.g\right)\) (vì có DE//BC)
\(\Rightarrow\dfrac{DE}{BC}=\dfrac{AE}{AC}\) (3)
\(\Delta AIE\sim\Delta AMC\left(g.g\right)\) (vì có IE//MC)
\(\Rightarrow\dfrac{IE}{MC}=\dfrac{AE}{AC}\) (4)
Từ (3) và (4) ta có: \(\dfrac{DE}{BC}=\dfrac{IE}{MC}\Rightarrow\dfrac{DE}{IE}=\dfrac{BC}{MC}=2\)
\(\Rightarrow DE=2IE\)
Hay I là trung điểm của DE


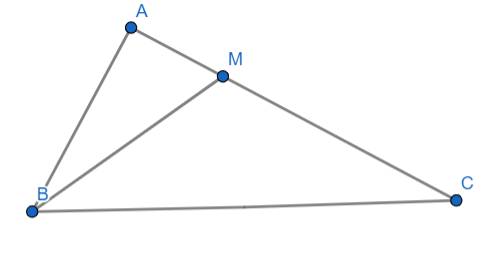
a) Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{10^2+20^2}=10\sqrt{5}\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác ABM vuông tại A ta có:
\(BM^2=AB^2+AM^2\)
\(\Rightarrow BM=\sqrt{AB^2+AM^2}\)
\(\Rightarrow BM=\sqrt{10^2+5^2}=5\sqrt{5}\left(cm\right)\)
b) Ta có:
\(\dfrac{AM}{AB}=\dfrac{1}{2}\)
\(\dfrac{BM}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
Xét hai tam giác ABC và AMB có:
\(\widehat{BAC}\) chung
\(\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\Delta ABC\sim\Delta AMB\left(c.g.c\right)\)

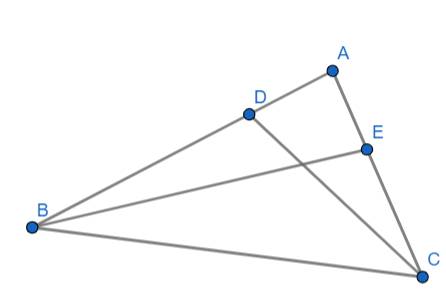
a) Xét hai tam giác ABE và ACD có:
\(\widehat{ACD}=\widehat{ABE}\left(gt\right)\)
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta ABE\sim\Delta ACD\left(g.g\right)\)
b) Ta có: \(\Delta ABE\sim\Delta ACD\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AE}{AD}\)

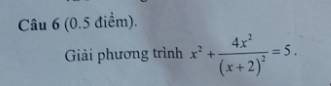

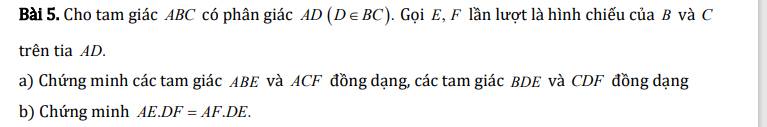
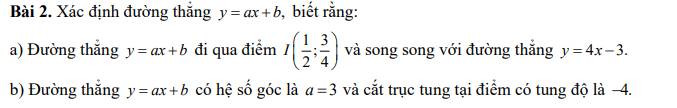


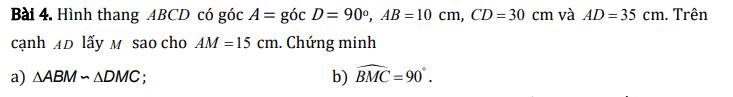
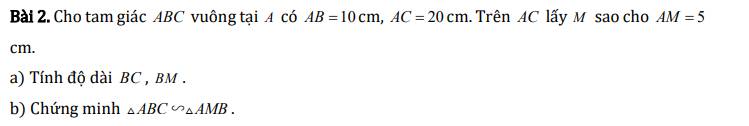
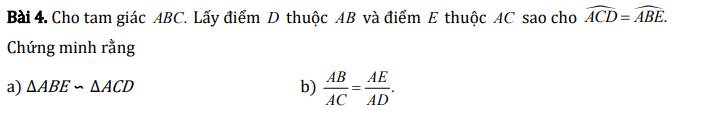

ĐKXĐ: x<>-2
\(x^2+\dfrac{4x^2}{\left(x+2\right)^2}=5\)
=>\(\dfrac{\left(x^2+2x\right)^2+4x^2}{\left(x+2\right)^2}=5\)
=>\(x^4+4x^3+4x^2+4x^2=5\left(x^2+4x+4\right)\)
=>\(x^4+4x^3+8x^2-5x^2-20x-20=0\)
=>\(x^4+4x^3+3x^2-20x-20=0\)
=>\(\left(x-2\right)\left(x+1\right)\left(x^2+5x+10\right)=0\)
mà \(x^2+5x+10>0\forall x\)
nên (x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)