
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số đèn mỗi ngày mà lớp 9A, số đèn mỗi ngày mà lớp 9B làm được lần lượt là a,b (đèn) (a,b>0)
=> Lớp 9A làm 2 ngày, lớp 9B làm 1 ngày được 22 chiếc, ta có pt: 2a+b=22 (1)
Lớp 9A làm 1 ngày, lớp 9B làm 2 ngày được 23 chiếc, ta có pt: a+2b=23 (2)
Từ (1), (2) lập hệ pt:
\(\left\{{}\begin{matrix}2a+b=22\\a+2b=23\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a+2b=44\\a+2b=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3a=21\\2a+b=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=22-2a\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=7\\a=22-2.7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=7\\a=8\end{matrix}\right.\)
Một ngày, cả 2 lớp cùng làm thì sẽ được: a+b=7+8=15(chiếc đèn)
Nếu cả hai lớp cùng làm thì thời gian hoàn thành công việc sẽ là:
60:15=4(ngày)

Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{3}< >-\dfrac{1}{m}\)
=>\(m^2\ne-3\)(luôn đúng)
Ta có: \(\left\{{}\begin{matrix}mx-y=2\\3x+my=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m\left(mx-2\right)=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m^2x-2m=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\x\left(m^2+3\right)=5m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=m\cdot\dfrac{5m}{m^2+3}-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=\dfrac{5m^2-2m^2-6}{m^2+3}=\dfrac{3m^2-6}{m^2+3}\end{matrix}\right.\)
\(\left(x+y\right)\cdot\left(m^2+3\right)+8=0\)
=>\(\dfrac{5m+3m^2-6}{m^2+3}\cdot\left(m^2+3\right)+8=0\)
=>\(3m^2+5m-6+8=0\)
=>\(3m^2+5m+2=0\)
=>(m+1)(3m+2)=0
=>\(\left[{}\begin{matrix}m=-1\\m=-\dfrac{2}{3}\end{matrix}\right.\)

b: Xét ΔAEB vuông tại E và ΔAKC vuông tại K có
\(\widehat{EAB}\) chung
Do đó: ΔAEB\(\sim\)ΔAKC
Suy ra: \(\dfrac{AE}{AK}=\dfrac{AB}{AC}\)
hay \(AK\cdot AB=AE\cdot AC\)

Bài 1:
a: ĐKXĐ: \(x\ge2\)
b: ĐKXĐ: \(x>\dfrac{1}{2}\)


4:
a: góc OBA+góc OCA=180 độ
=>OBAC nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AB^2=AH*AO


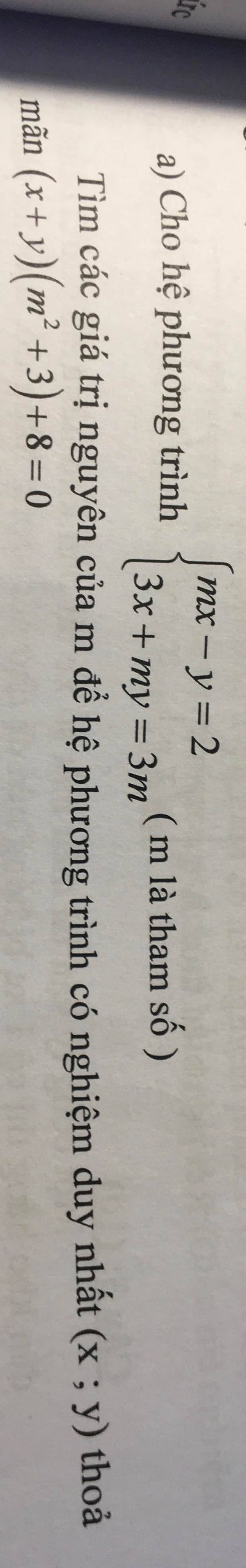
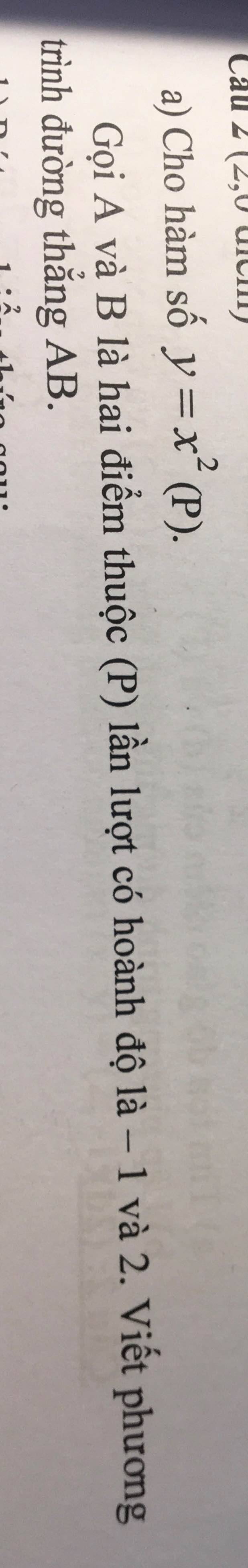
 giúp mình câu 4 với câu 2 phần 2 với
giúp mình câu 4 với câu 2 phần 2 với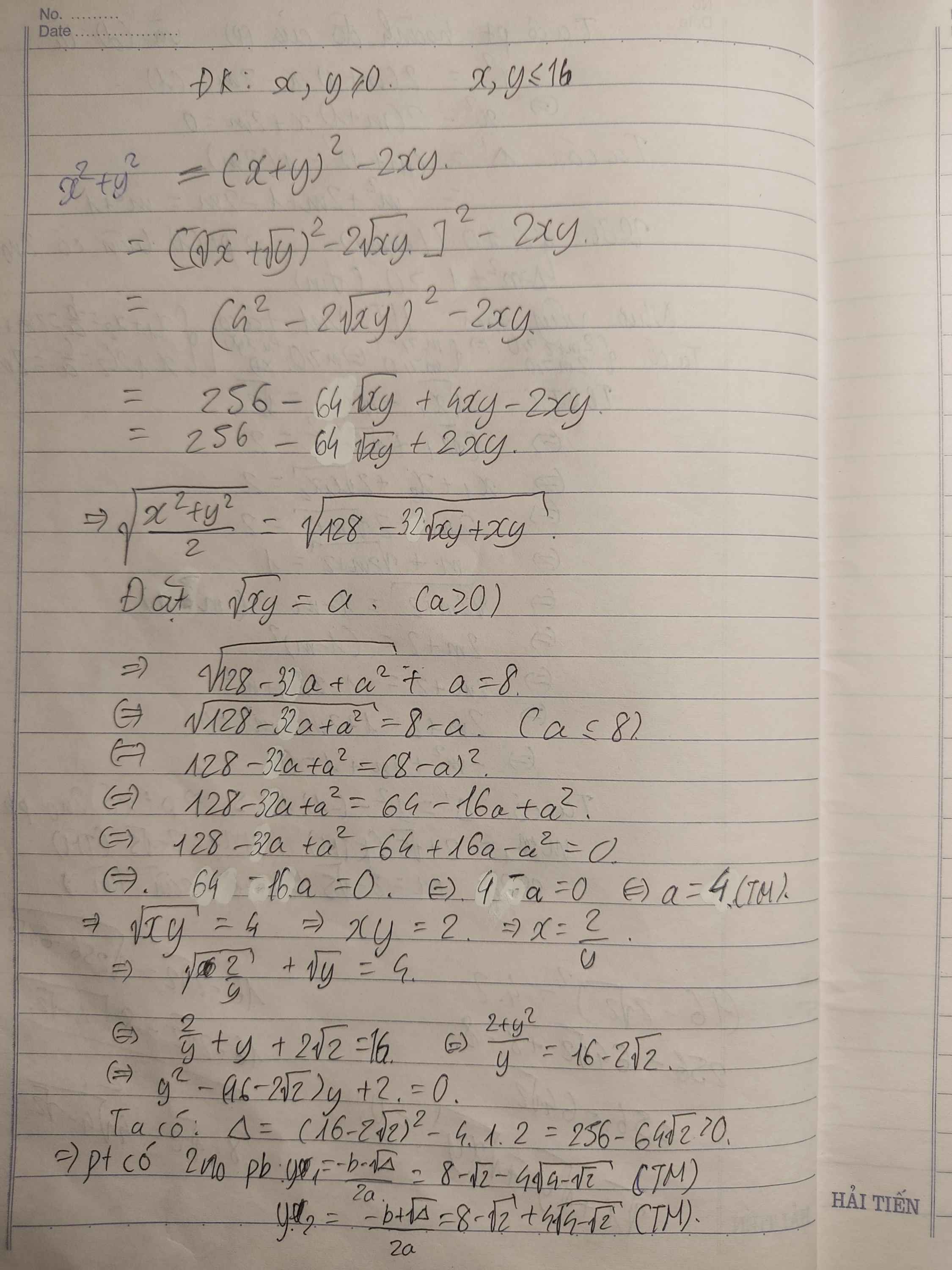
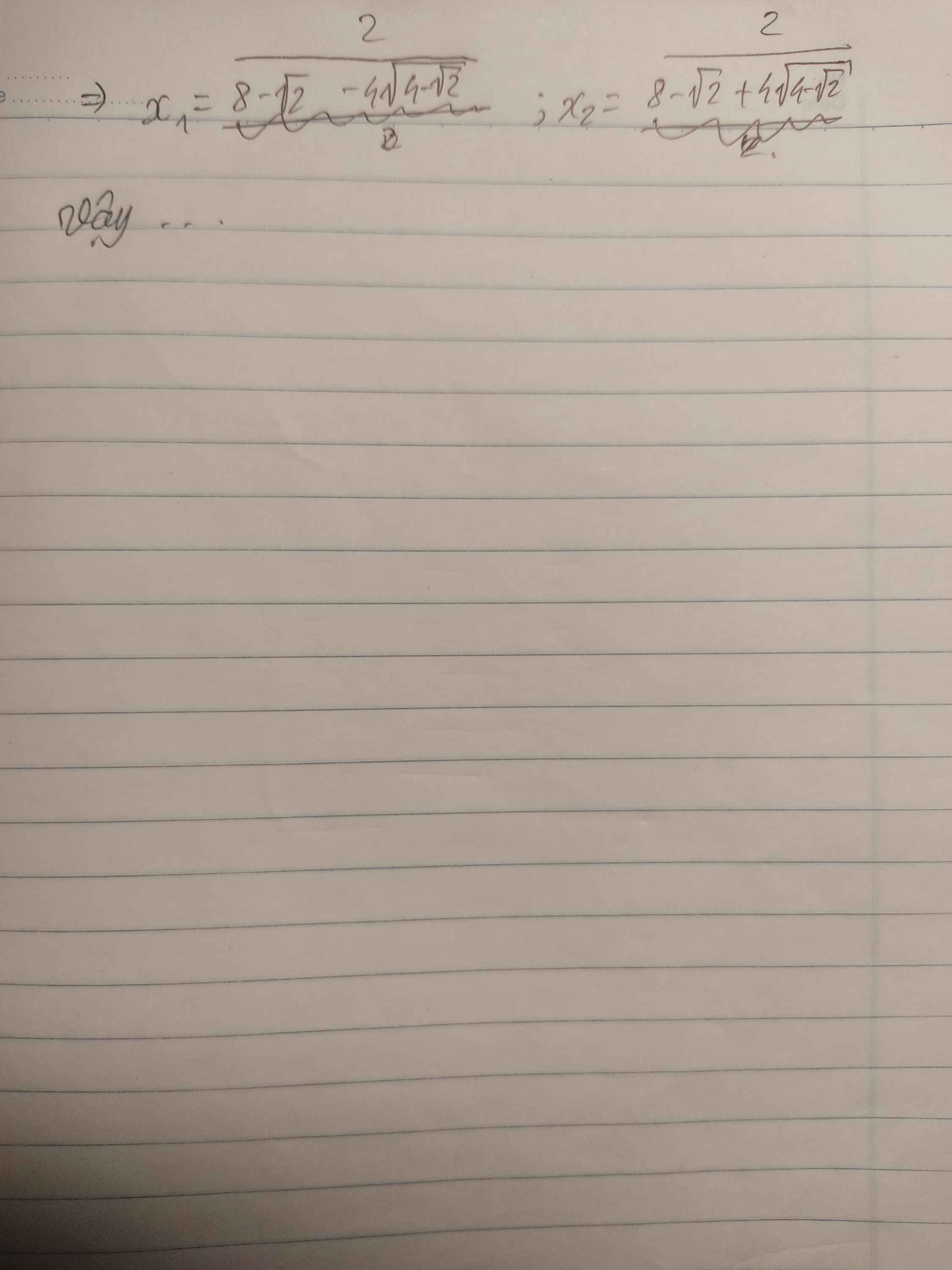


 Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!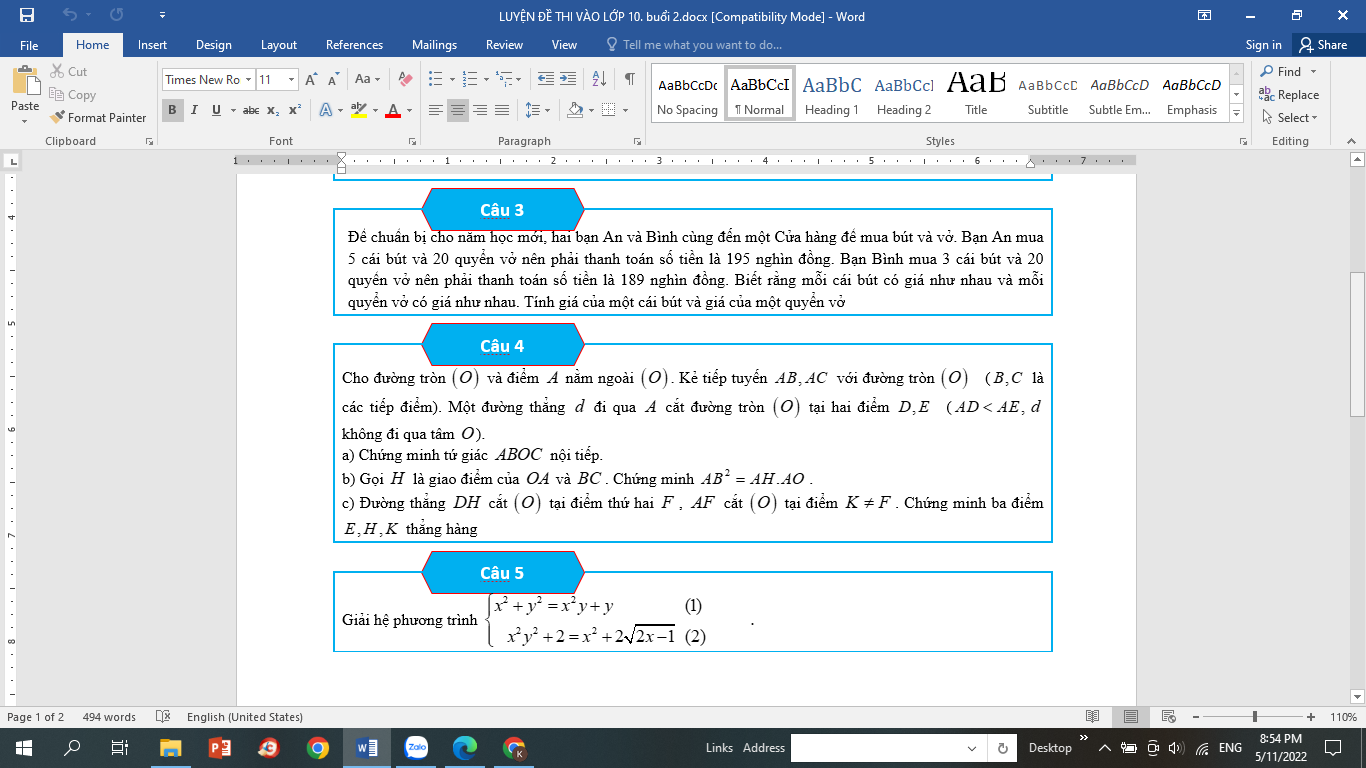

\(B=\dfrac{5x+15\sqrt{x}-26\sqrt{x}+26-20}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{5x-11\sqrt{x}+6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(5\sqrt{x}-6\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{5\sqrt{x}-6}{\sqrt{x}+3}\)
n: \(B< =\dfrac{-x+9\sqrt{x}-10}{\sqrt{x}+3}\)
=>5*căn x-6<=-x+9căn x-10
=>x-4*căn x+4<=0
=>(căn x-2)^2<=0
=>căn x-2=0
=>x=4
p: \(B=\dfrac{5\sqrt{x}+15-21}{\sqrt{x}+3}=5-\dfrac{21}{\sqrt{x}+3}\)
căn x+3>=3
=>21/căn x+3<=7
=>-21/căn x+3>=-7
=>B>=-7+5=-2
Dấu = xảy ra khi x=0