K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 8 2021
X³-4x+x-2=x×(x²-4)+(x-2)
=x×(x-2)×(x+2)+(x-2)
=(x-2)×(x×(x+2)+1)
1 tháng 9 2021
\(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-8=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-8\)
Đặt \(x^2+7x=t\)
\(\left(t+10\right)\left(t+12\right)-8=t^2+22t+120-8\)
\(=t^2+22t+112=\left(t+8\right)\left(t+14\right)\)
Theo cách đặt \(=\left(x^2+7x+8\right)\left(x^2+7x+14\right)\)
28 tháng 8 2021
a) -4x2 + 8x - 4
= - (4x2 - 8x + 4)
= - (2x - 2)2
b) -x52 + 10 x - 5
= - 5(x2 - 2x + 1)
= - 5(x - 1)2
VD
29 tháng 5 2022
Hướng dẫn: A đạt GTLN khi \(\dfrac{1}{A}\) đạt GTNN
Ta có: \(x^2+2\ge0\forall x\)
\(\Rightarrow A=\dfrac{1}{x^2+2}\le\dfrac{1}{2}\forall x\)
Vậy GTLN của A là 1/2
=> A
2 tháng 9 2021
\(\frac{3\left(x-2\right)}{4}\div\frac{2-x}{2}=\frac{3\left(x-2\right)}{4}\times\frac{-2}{x-2}=\frac{-3}{2}\)
học tốt
2 tháng 9 2021
Rút gọn nhé !
\(\frac{3}{4}.\left(x-2\right):\frac{1}{2}.\left(2-x\right)=\frac{3x-6}{4}.2.\left(2-x\right)\)
\(=\frac{3x-6}{4}.\left(4-2x\right)=\frac{\left(3x-6\right).\left(4-2x\right)}{4}\)
\(=\frac{\left(12x-24\right)-\left(6x^2+12x\right)}{4}=\frac{-24-6x^2}{4}\)
\(=\frac{-12-3x^2}{2}=\frac{-3.\left(4+x^2\right)}{2}\)
8 tháng 8 2023
4.2:
a: x^2-x+1=x^2-x+1/4+3/4
=(x-1/2)^2+3/4>=3/4>0 với mọi x
=>x^2-x+1 ko có nghiệm
b: 3x-x^2-4
=-(x^2-3x+4)
=-(x^2-3x+9/4+7/4)
=-(x-3/2)^2-7/4<=-7/4<0 với mọi x
=>3x-x^2-4 ko có nghiệm
5:
a: x^2+y^2=25
x^2-y^2=7
=>x^2=(25+7)/2=16 và y^2=16-7=9
x^4+y^4=(x^2)^2+(y^2)^2
=16^2+9^2
=256+81
=337
b: x^2+y^2=(x+y)^2-2xy
=1^2-2*(-6)
=1+12=13
x^3+y^3=(x+y)^3-3xy(x+y)
=1^3-3*1*(-6)
=1+18=19
14 tháng 4 2022
a: 3-21x=0
=>21x=3
hay x=1/7
b: \(9x\left(x-1\right)+12=x+\left(3x+2\right)^2\)
\(\Leftrightarrow9x^2-9x+12-x-9x^2-12x-4=0\)
=>-22x+8=0
=>-22x=-8
hay x=4/11
c: \(\Leftrightarrow8\left(x+3\right)-5\left(1-2x\right)=4x\)
=>8x+24-5+10x=4x
=>14x-4x=-19
hay x=-19/5
HK
1
29 tháng 10 2020
a) x2 - 9 = 3( x - 3 )
⇔ ( x - 3 )( x + 3 ) - 3( x - 3 ) = 0
⇔ ( x - 3 )( x + 3 - 3 ) = 0
⇔ ( x - 3 ).x = 0
⇔ x - 3 = 0 hoặc x = 0
⇔ x = 3 hoặc x = 0
b) 3( 3x2 + 1 ) = 6 - 2( 3x + 2 )
⇔ 9x2 + 3 = 6 - 6x - 4
⇔ 9x2 + 6x + 3 - 6 + 4 = 0
⇔ 9x2 + 6x + 1 = 0
⇔ ( 3x + 1 )2 = 0
⇔ 3x + 1 = 0
⇔ x = -1/3
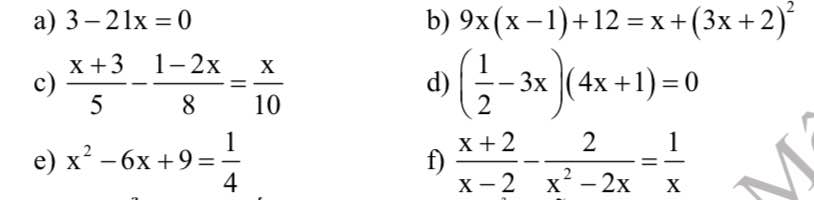
Answer:
a) Ta thay \(x=-3\) vào biểu thức B
\(B=\frac{-3+2}{3.\left(-3\right)+2}=\frac{-1}{-7}=\frac{1}{7}\)
b) \(A=\frac{1}{x+2}-\frac{2x}{4-x^2}+\frac{3}{x-2}=\frac{x-2+2x+3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\frac{3x-2+3x+6}{\left(x-2\right)\left(x+2\right)}=\frac{6x+4}{\left(x-2\right)\left(x+2\right)}\)
\(M=A.B=\frac{6x+4}{\left(x-2\right)\left(x+2\right)}.\frac{x+2}{3x+2}=\frac{2\left(3x+2\right)}{\left(x-2\right)\left(x+2\right)}.\frac{x+2}{3x+2}=\frac{2}{x-2}\)
c) \(N=M.\left(x^3-x^2-2x\right)=\frac{2}{x-2}.x\left(x^2-x-2\right)=2x\left(x+1\right)=2\left(x^2+2x.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}\right)=2\left(x+\frac{1}{2}\right)^2-\frac{1}{2}\)
Mà \(2\left(x+\frac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x+\frac{1}{2}\right)^2-\frac{1}{2}\ge\frac{-1}{2}\)
Vậy giá trị nhỏ nhất bằng \(\frac{-1}{2}\) khi \(x=\frac{-1}{2}\)
trả lời sớm hơn thì tốt quá