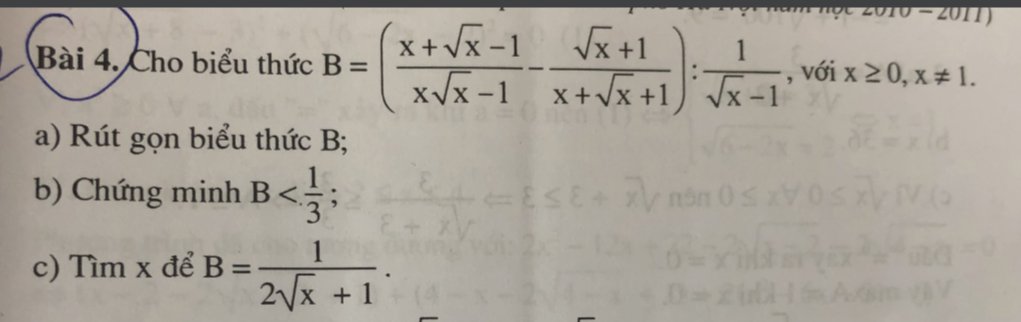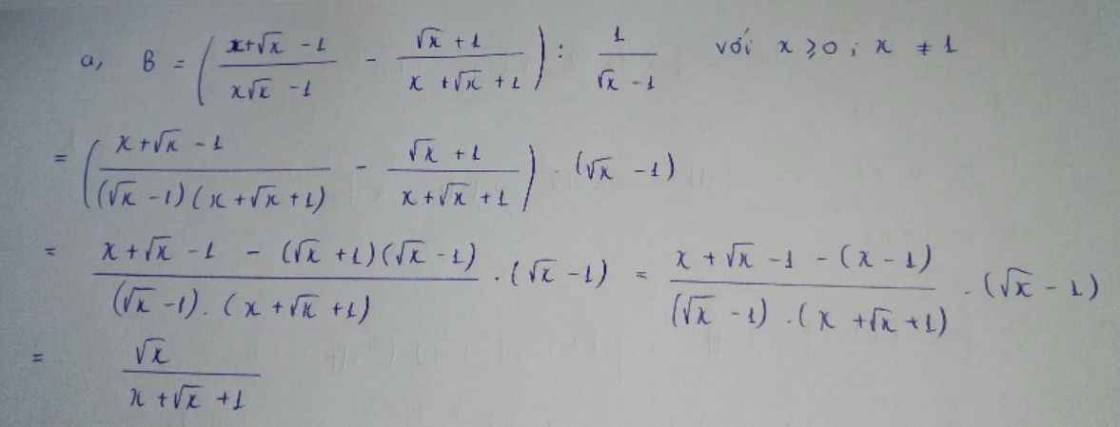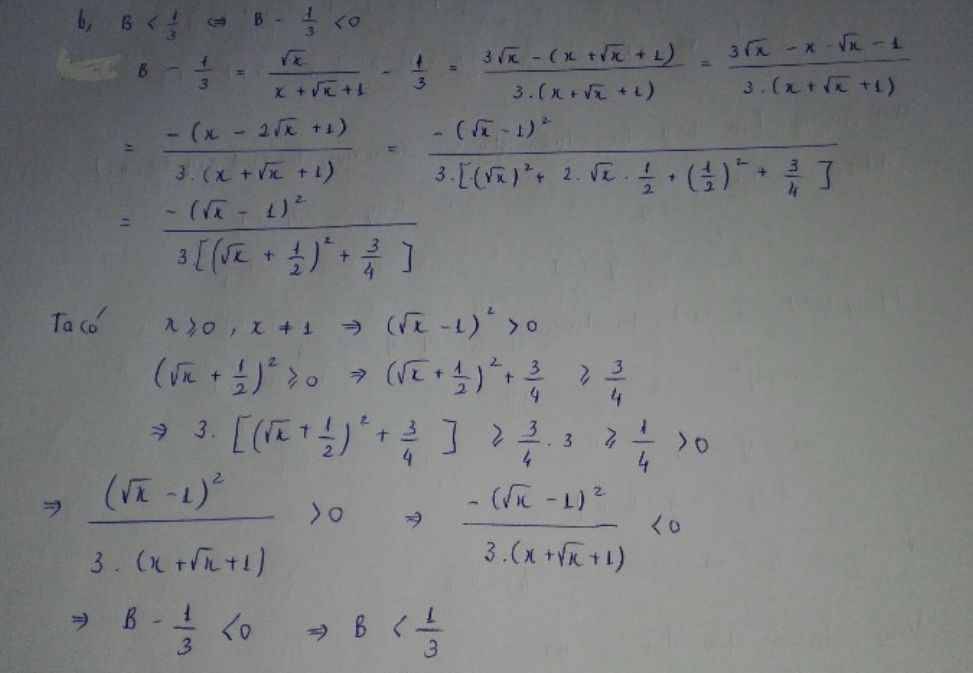K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AT
15 tháng 7 2021
a) \(P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\left(x>0,x\ne1\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}+\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\sqrt{x}\left(\sqrt{x}-1\right)-\left(2\sqrt{x}+1\right)+2\left(\sqrt{x}+1\right)=x-\sqrt{x}+1\)
b) \(P=x-\sqrt{x}+1=\left(\sqrt{x}\right)^2-2.\sqrt{x}.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
\(=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(\Rightarrow P_{min}=\dfrac{3}{4}\) khi \(x=\dfrac{1}{4}\)
c) \(Q=\dfrac{2\sqrt{x}}{P}=\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}\)
Ta có: \(\left\{{}\begin{matrix}2\sqrt{x}>0\left(x>0\right)\\x+\sqrt{x}+1>0\end{matrix}\right.\Rightarrow Q>0\)
Lại có: \(3x-5\sqrt{x}+3=3\left(\left(\sqrt{x}\right)^2-2.\sqrt{x}.\dfrac{5}{6}+\left(\dfrac{5}{6}\right)^2\right)+\dfrac{11}{12}\)
\(=3\left(\sqrt{x}-\dfrac{5}{6}\right)^2+\dfrac{11}{12}>0\)
\(\Rightarrow3x-5\sqrt{x}+3>0\Rightarrow3x-3\sqrt{x}+3>2\sqrt{x}\Rightarrow3\left(x-\sqrt{x}+1\right)>2\sqrt{x}\)
\(\Rightarrow3>\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}\Rightarrow Q< 3\Rightarrow0< Q< 3\)
mà \(Q\in Z\Rightarrow Q\in\left\{1;2\right\}\)
Từ\(Q\) tính ta x thôi
15 tháng 7 2021
a, \(P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)ĐK : \(x>0;x\ne1\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}-\dfrac{2\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}+\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=x-\sqrt{x}-2\left(\sqrt{x}+1\right)+2\left(\sqrt{x}+1\right)=x-\sqrt{x}-2\sqrt{x}-2+2\sqrt{x}+2\)
\(=x-\sqrt{x}\)
b, Ta có : \(x-\sqrt{x}+\dfrac{1}{4}-\dfrac{1}{4}=\left(\sqrt{x}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
Dấu ''='' xảy ra khi \(x=\dfrac{1}{4}\)
Vậy GTNN P là -1/4 khi x = 1/4
c, Ta có : \(G=\dfrac{2\sqrt{x}}{P}\Rightarrow G=\dfrac{2\sqrt{x}}{x-\sqrt{x}}=\dfrac{2}{\sqrt{x}-1}\)
\(\Rightarrow\sqrt{x}-1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
| \(\sqrt{x}-1\) | 1 | -1 | 2 | -2 |
| \(\sqrt{x}\) | 2 | 0 | 3 | -1 |
| x | 4 | 0 ( loại ) | 9 | loại |
20 tháng 11 2021
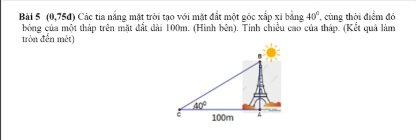
\(AB=\tan C\cdot AC=\tan40^0\cdot100\approx84\left(m\right)\)
HL
2
29 tháng 10 2023
a: \(\dfrac{4\sqrt{6}-2\sqrt{10}}{2\sqrt{2}}+\dfrac{4}{\sqrt{3}-\sqrt{5}}+3\sqrt{6-2\sqrt{5}}\)
\(=\dfrac{2\sqrt{2}\left(2\sqrt{3}-\sqrt{5}\right)}{2\sqrt{2}}-\dfrac{4\left(\sqrt{5}+\sqrt{3}\right)}{5-3}+3\sqrt{\left(\sqrt{5}-1\right)^2}\)
\(=2\sqrt{3}-\sqrt{5}-2\left(\sqrt{5}+\sqrt{3}\right)+3\left(\sqrt{5}-1\right)\)
\(=2\sqrt{3}-\sqrt{5}-2\sqrt{5}-2\sqrt{3}+3\sqrt{5}-3\)
=-3
b: \(\dfrac{x-1}{\sqrt{y}-1}\cdot\sqrt{\dfrac{y-2\sqrt{y}+1}{\left(x-1\right)^4}}\)
\(=\dfrac{x-1}{\sqrt{y}-1}\cdot\left|\dfrac{\sqrt{y}-1}{\left(x-1\right)^2}\right|\)
\(=\dfrac{x-1}{\sqrt{y}-1}\cdot\dfrac{\left|\sqrt{y}-1\right|}{\left(x-1\right)^2}=\pm\dfrac{1}{x-1}\)
TM
29 tháng 10 2023
a, \(\dfrac{4\sqrt{6}-2\sqrt{10}}{2\sqrt{2}}+\dfrac{4}{\sqrt{3}-\sqrt{5}}+3\sqrt{6-2\sqrt{5}}\)
\(=\dfrac{2\sqrt{2}\left(2\sqrt{3}-\sqrt{5}\right)}{2\sqrt{2}}+\dfrac{4\left(\sqrt{3}+\sqrt{5}\right)}{\left(\sqrt{3}-\sqrt{5}\right)\left(\sqrt{3}+\sqrt{5}\right)}+3\sqrt{\left(\sqrt{5}-1\right)^2}\)
\(=2\sqrt{3}-\sqrt{5}+\dfrac{4\sqrt{3}+4\sqrt{5}}{3-5}+3\left|\sqrt{5}-1\right|\)
\(=2\sqrt{3}-\sqrt{5}-2\sqrt{3}-2\sqrt{5}+3\sqrt{5}-3\)
\(=-3\)
b, \(với\left(x\ne1;y\ne1;y\ge0\right)\)
\(\dfrac{x-1}{\sqrt{y}-1}\sqrt{\dfrac{y-2\sqrt{y}+1}{\left(x-1\right)^4}}=\dfrac{x-1}{\sqrt{y}-1}\dfrac{\sqrt{\left(\sqrt{y}-1\right)^2}}{\left(x-1\right)^2}=\dfrac{\left|\sqrt{y}-1\right|}{\left(\sqrt{y}-1\right)\left(x-1\right)}\left(1\right)\)
\(TH1:y>1\)
\(\left(1\right)=\dfrac{\sqrt{y}-1}{\left(\sqrt{y}-1\right)\left(x-1\right)}=\dfrac{1}{x-1}\)
\(TH2:0\le y< 1\)
\(\left(1\right)=\dfrac{1-\sqrt{y}}{\left(\sqrt{y}-1\right)\left(x-1\right)}=\dfrac{-1}{x-1}\)
14 tháng 10 2021
a: Xét (O) có
ΔAMB nội tiếp đường tròn
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét tứ giác AMCK có
\(\widehat{AKC}+\widehat{AMC}=180^0\)
nên AMCK là tứ giác nội tiếp
hay A,M,C,K cùng thuộc một đường tròn
7 tháng 7 2021
1,\(\sqrt{\left(x-1\right)^2}=\left|x-1\right|=-\left(x-1\right)=1-x\)
2,\(\sqrt{\left(a-2b\right)^2}=\left|a-2b\right|=-\left(a-2b\right)=2b-a\)
3,\(\sqrt{\left(2x-1\right)^2}=\left|2x-1\right|=2x-1\)
14 tháng 10 2021
bạn tự vẽ hình giúp mik nha
a.ta có \(\Delta\)ABC nội tiếp (O) và AB là đường kính nên \(\Delta\)ABC vuông tại C
trong \(\Delta ABC\) vuông tại C có
AC=AB.cosBAC=10.cos30=8,7
BC=AB.sinCAB=10.sin30=5
ta có Bx là tiếp tuyến của (O) nên Bx vuông góc với AB tại B
trong \(\Delta\)ABE vuông tại B có
\(cosBAE=\dfrac{AB}{AE}\Rightarrow AE=\dfrac{AB}{cosBAE}=\dfrac{10}{cos30}=11,5\)
mà:CE=AE-AC=11,5-8,7=2,8
b.áp dụng pytago vào \(\Delta ABE\) vuông tại B có
\(BE=\sqrt{AE^2-AB^2}=\sqrt{11,5^2-10^2}=5,7\)
25 tháng 5 2021
`1)((sqrt{14}-sqrt7)/(1-sqrt2)+(sqrt{15}-sqrt5)/(1-sqrt3)):1/(sqrt7-sqrt5)`
`=((sqrt7(sqrt2-1))/(1-sqrt2)+(sqrt5(sqrt3-1))/(1-sqrt3):1/(sqrt7-sqrt5)`
`=(-sqrt7-sqrt5):1/(sqrt7-sqrt5)`
`=-(sqrt7+sqrt5).(sqrt7-sqrt5)`
`=-(7-5)`
`=-2`
`2)B=(2sqrtx-9)/(x-5sqrtx+6)-(sqrtx+3)/(sqrtx-2)-(2sqrtx+1)/(3-sqrtx)`
`=(2sqrtx-9-x+9+2x-3sqrtx-2)/(x-5sqrtx+6)`
`=(x-sqrtx-2)/(x-5sqrtx+6)`
`=((sqrtx-2)(sqrtx+1))/((sqrtx-2)(sqrtx-3))`
`=(sqrtx+1)/(sqrtx-3)`
`x=11+6sqrt2`
`=(3+sqrt2)^2`
`=>B=(4+2sqrt2)/(sqrt2)`
`=2+2sqrt2`
25 tháng 5 2021
`3)5x^4+4x^2-1=0`
Đặt `t=x^2(t>=0)`
`pt<=>5t^2+4t-1=0`
`a-b+c=0`
`=>t_1=-1(l),t_2=1/5(tm)`
`<=>x=+-sqrt{1/5}`
Vậy `S={-sqrt{1/5},+sqrt{1/5}}`