Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo bài tương tự mà mình làm đây nhé:
Bài 1:

Bạn thay điểm E thành điểm F và điểm K thành điểm E nhé.
a)
Xét tam giác ABM và tam giác ADM có:
AB = AD (gt)
BM = DM (vì M là trung điểm của BD)
AM là cạnh chung
=> Tam giác ABM = Tam giác ADM (c . c . c)
b) Xét tam giác ABD có:
AB = AD (gt)
=> Tam giác ABD cân tại A.
Có M là trung điểm của BD
=> AM là đường trung tuyến của tam giác ABD.
=> AM đồng thời là đường trung trực của tam giác ABD.
=> AM là đường trung trực của đoạn thẳng BD.
c) Theo câu b) ta có tam giác ABM = tam giác ADM.
=> BAM = DAM (2 góc tương ứng)
Hay BAE = DAE.
Xét tam giác ABE và tam giác ADE có:
AB = AD (gt)
BAE = DAE (cmt)
AE là cạnh chung
=> Tam giác ABE = Tam giác ADE (c . g . c)
=> ABE = ADE (2 góc tương ứng).
=> BE = DE (2 cạnh tương ứng).
Ta có:
ABE + EBF = 1800 (vì 2 góc kề bù)
ADE + EDC = 1800 (vì 2 góc kề bù)
Mà ABE = ADE (cmt)
=> EBF = EDC.
Xét tam giác EBF và tam giác EDC có:
EB = ED (cmt)
EBF = EDC (cmt)
BF = DC (gt)
=> Tam giác EBF = Tam giác EDC (c . g . c)
=> BEF = DEC (2 góc tương ứng)
Lại có: BED + DEC = 180 (2 góc kề bù)
Mà BEF = DEC (cmt).
=> BED + BEF = 1800
Mà BED + BEF = FED.
=> FED = 1800
=> E, F, D thẳng hàng (đpcm).
Chúc bạn học tốt!

Bạn đừng để ý đến điểm I và J nhé.
a) Xét 2 \(\Delta\) \(ABC\) và \(ADE\) có:
\(AB=AD\left(gt\right)\)
\(AC=AE\left(gt\right)\)
\(\widehat{BAC}=\widehat{DAE}\) (vì 2 góc đối đỉnh)
=> \(\Delta ABC=\Delta ADE\left(c-g-c\right).\)
b) Theo câu a) ta có \(\Delta ABC=\Delta ADE.\)
=> \(\widehat{ABC}=\widehat{ADE}\) (2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong.
=> \(BC\) // \(DE\left(đpcm\right).\)
Chúc bạn học tốt!

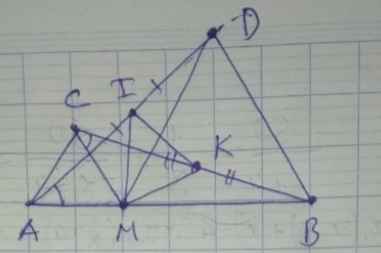
a) Ta có: \(\widehat{AMD}=\widehat{AMC}+\widehat{CMD}\)
\(=60^0+\widehat{CMD}\) \(\left(1\right)\)
Lại có: \(\widehat{CMB}=\widehat{BMD}+\widehat{CAD}\)
\(=60^0+\widehat{CMD}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\): ⇒ \(\widehat{AMD}=\widehat{CMB}\)
Xét △ AMD và △ CMB có:
CH = AM ( △ AMC đều )
\(\widehat{AMD}=\widehat{CMB}\) ( cmt )
MB = MD ( △ BMD đều )
⇒ △ AMD = △ CMB ( c - g - c )
Do đó: AD = CB ( 2 cạnh tương ứng )
b) Ta có: \(CK=\dfrac{BC}{2}\) ( K là trung điểm CB )
Ta có: \(AI=\dfrac{AD}{2}\) ( I là trung điểm AD )
Mà BC = AD ( cmt ) ⇒ CK = AI
Xét △ AMI và △ CMK có:
CM = AM ( △ AMC đều )
\(\widehat{IAM}=\widehat{KCM}\) ( vì △ AMD = △ CMB )
AI = CK ( cmt )
⇒ △ AMI = △ CMK ( c - g - c )
⇒ MK = MI
⇒ △ IMK cân tại M
Bài 1:
Mình có hình cho câu a) thôi nha.
a) Xét 2 \(\Delta\) \(ABD\) và \(ACD\) có:
\(AB=AC\left(gt\right)\)
\(BD=CD\) (vì D là trung điểm của \(BC\))
Cạnh AD chung
=> \(\Delta ABD=\Delta ACD\left(c-c-c\right)\)
=> \(\widehat{BAD}=\widehat{CAD}\) (2 góc tương ứng).
=> \(AD\) là tia phân giác của \(\widehat{BAC}.\)
b) Vì \(\widehat{BAD}=\widehat{CAD}\left(cmt\right)\)
=> \(\widehat{MAD}=\widehat{NAD}.\)
Xét 2 \(\Delta\) \(AMD\) và \(AND\) có:
\(AM=AN\left(gt\right)\)
\(\widehat{MAD}=\widehat{NAD}\left(cmt\right)\)
Cạnh AD chung
=> \(\Delta AMD=\Delta AND\left(c-g-c\right)\)
=> \(\widehat{AMD}=\widehat{AND}\) (2 góc tương ứng).
Mà \(\widehat{AMD}=90^0\left(gt\right)\)
=> \(\widehat{AND}=90^0.\)
=> \(DN\perp AN\)
Hay \(DN\perp AC.\)
Chúc bạn học tốt!