
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


giúp mik zới, chỉ cần thay số vào thôi mà, mik chỉ kiểm tra đáp án xem có đúng hay ko thôi
Thay \(x=2;y=-1\)vào A ta được
\(A=4-3\left(-1\right)+4.4=4+3+16=23\)

Bài 8:
a: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc với BC và M là trung điểm của BC
b: Xét ΔMAB vuông tại M và ΔMDC vuông tại M có
MB=MC
góc MBA=góc MCD
Do đo: ΔMAB=ΔMDC
=>MA=MD
=>M là trung điểm của AD

a: Xét ΔBAE và ΔBDE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBAE=ΔBDE
b: Ta có: ΔBAE=ΔBDE
nên \(\widehat{BAE}=\widehat{BDE}=90^0\)
hay ED\(\perp\)BC
c: Xét ΔAKE vuông tại A và ΔDCE vuông tại D có
EA=ED
\(\widehat{AEK}=\widehat{DEC}\)
Do đó: ΔAKE=ΔDCE
Suy ra: EK=EC
hay ΔEKC cân tại E


Bài 1:
c: Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=3k\\y=4k\end{matrix}\right.\)
Ta có: xy=48
\(\Leftrightarrow12k^2=48\)
\(\Leftrightarrow k^2=4\)
Trường hợp 1: k=2
\(\Leftrightarrow\left\{{}\begin{matrix}y=3k=3\cdot2=6\\y=4k=4\cdot2=8\end{matrix}\right.\)
Trường hợp 2: k=-2
\(\Leftrightarrow\left\{{}\begin{matrix}y=3k=3\cdot\left(-2\right)=-6\\y=4k=4\cdot\left(-2\right)=-8\end{matrix}\right.\)
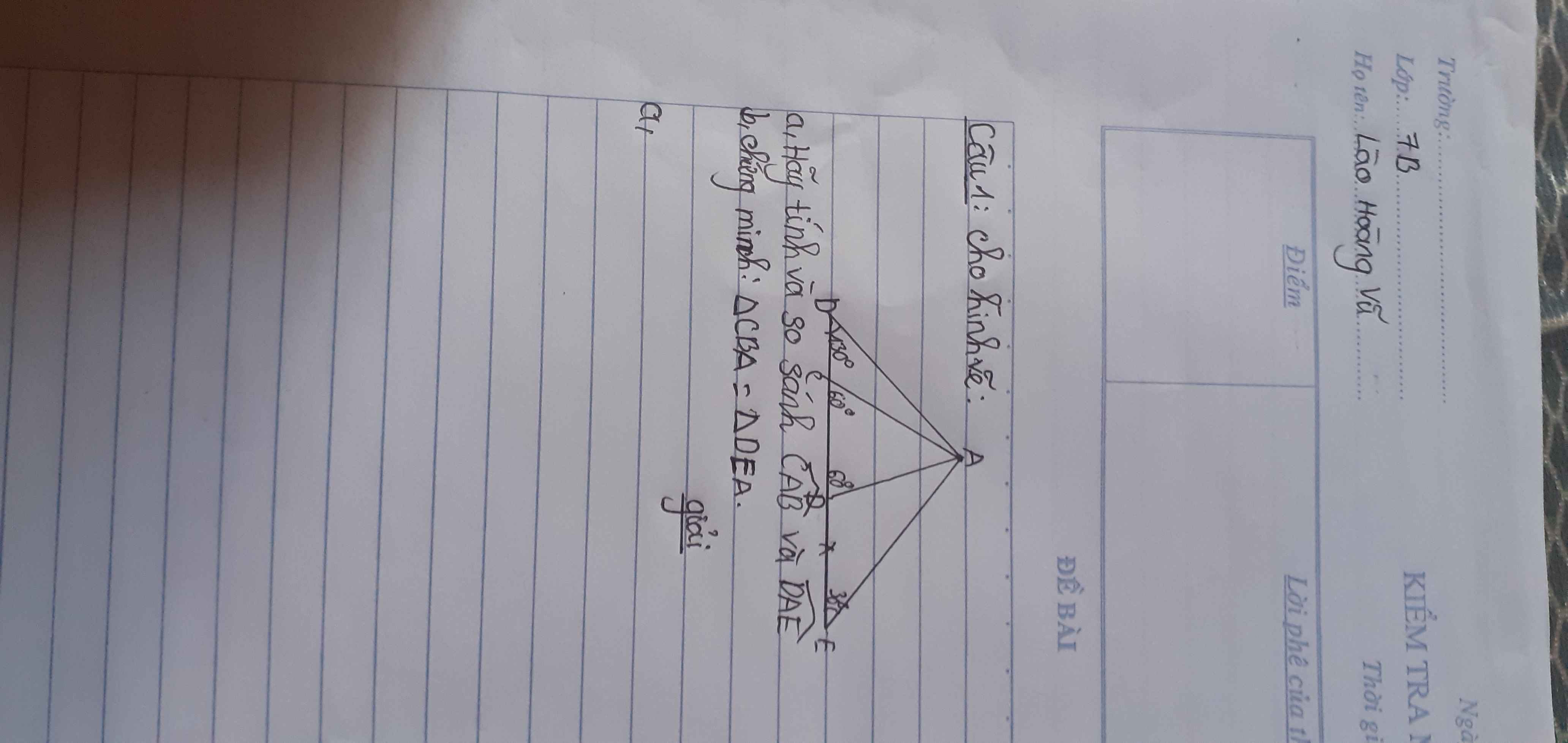
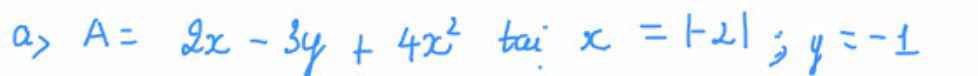

 giup mik voi mik cam on!
giup mik voi mik cam on!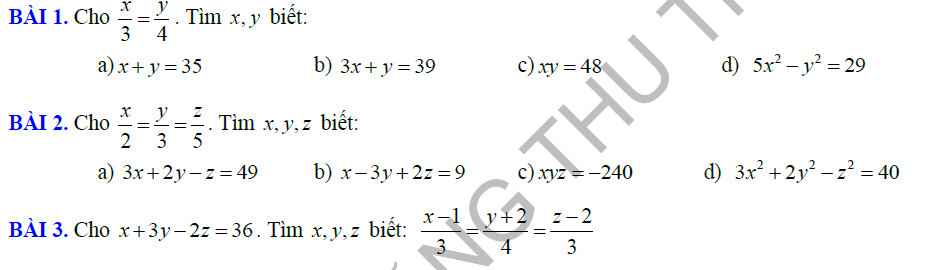
\(a,A=\frac{1}{2}-\frac{1}{3}=\frac{1}{6};B=\frac{1}{3}-\frac{1}{4}=\frac{1}{12};C=\frac{1}{4}-\frac{1}{5}=\frac{1}{20}\)
\(b,A+B=\frac{1}{6}+\frac{1}{12}=\frac{3}{12}=\frac{1}{4};A+B+C=\frac{1}{6}+\frac{1}{12}+\frac{1}{20}=\frac{10+5+3}{60}=\frac{18}{60}=\frac{3}{10}\)
\(c,D=\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+...+\frac{1}{19\cdot20}=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{19}-\frac{1}{20}\)
\(=\frac{1}{2}-\frac{1}{20}=\frac{9}{20}\)
\(E=\frac{1}{99}-\frac{1}{99\cdot98}-\frac{1}{98\cdot97}-\frac{1}{97\cdot96}-...-\frac{1}{3\cdot2}-\frac{1}{2\cdot1}\)
\(=-\left(-\frac{1}{99}+\frac{1}{99\cdot98}+\frac{1}{98\cdot97}+\frac{1}{97\cdot96}+...+\frac{1}{3\cdot2}+\frac{1}{2\cdot1}\right)\)
\(=-\left(-\frac{1}{99}+\frac{1}{99}-\frac{1}{98}+\frac{1}{98}-\frac{1}{97}+\frac{1}{97}-\frac{1}{96}+...+\frac{1}{3}-\frac{1}{2}+\frac{1}{2}-1\right)\)
\(=-\left(-\frac{1}{99}-1\right)=-\left(-\frac{100}{99}\right)=\frac{100}{99}\)