giúp mik câu này ddi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VT
3 tháng 1 2022
2xy - 3x + 5y=4
2x(y-1) + 5y = 4
2x(y-1) + 5y - 5 = 4 - 5
2x(y-1) - 1(y-1) = -1
(2x-1)(y-1) = -1
Ta thấy -1= (-1).1 => Ta có bảng sau:
| 2x-1 | -1 | 1 |
| y-1 | 1 | -1 |
| x | 0 | 1 |
| y | 2 | 0 |
Như vậy, ta có 2 trường hợp (x;y) thỏa mãn yêu cầu đề bài là ( 0;2 ) ; ( 1;0 )
Hok tốt~
20 tháng 8 2021
Ta có: \(C=\left(4x+y\right)\left(x^2-5xy+1\right)\)
\(=4x^3-20x^2y+4x-x^2y-5xy^2+y\)
\(=4x^3-21x^2y-5xy^2+4x+y\)
\(=4\cdot\dfrac{1}{8}-21\cdot\dfrac{1}{4}\cdot\dfrac{-1}{5}-5\cdot\dfrac{1}{2}\cdot\dfrac{1}{25}+4\cdot\dfrac{1}{2}+\dfrac{-1}{5}\)
\(=\dfrac{13}{4}\)
30 tháng 10 2021
Áp dụng t/c dtsbn:
\(\dfrac{2021a+b+c}{a}=\dfrac{a+2021b+c}{b}=\dfrac{a+b+2021c}{c}=\dfrac{2023\left(a+b+c\right)}{a+b+c}=2023\)
\(\Rightarrow\left\{{}\begin{matrix}2023a=2021a+b+c\\2023b=a+2021b+c\\2023c=a+b+2021c\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}2a=b+c\\2b=a+c\\2c=a+b\end{matrix}\right.\)
\(S=\dfrac{a+b}{c}+\dfrac{b+c}{a}+\dfrac{c+a}{b}=\dfrac{2c}{c}+\dfrac{2a}{a}+\dfrac{2b}{b}=2+2+2=6\)
HT
2
23 tháng 8 2018
\(\frac{2}{5}-\frac{1}{2}\left(x+\frac{1}{3}\right)=\frac{7}{5}\)
\(\frac{1}{2}\left(x+\frac{1}{3}\right)=\frac{2}{5}-\frac{7}{5}\)
\(\frac{1}{2}\left(x+\frac{1}{3}\right)=-1\)
\(x+\frac{1}{3}=-1:\frac{1}{2}\)
\(x+\frac{1}{3}=-2\)
\(x=-2-\frac{1}{3}\)
\(x=-\frac{7}{3}\)
23 tháng 8 2018
\(\frac{2}{5}-\frac{1}{2}.\left(x+\frac{1}{3}\right)=\frac{7}{5}\)
\(\Rightarrow\frac{1}{2}.\left(x+\frac{1}{3}\right)=\frac{2}{5}-\frac{7}{5}\)
\(\Rightarrow\frac{1}{2}.\left(x+\frac{1}{3}\right)=-1\)
\(\Rightarrow x+\frac{1}{3}=-2\)
\(\Rightarrow x=-\frac{7}{3}\)
VN
3
DT
4
29 tháng 6 2018
Bạn thêm vào chỗ này nhé, mình nhìn nhầm
\(\left(-3\right)^{18}=3^{18}=\left(3^2\right)^9=9^9\)
Đến đây làm tiếp tục như mình làm ở bài trước
Chúc bạn học tốt ~
29 tháng 6 2018
Ta có :
\(2^{27}=\left(2^3\right)^9=8^9\)
\(3^{18}=\left(3^2\right)^9=9^9\)
Vì \(8^9< 9^9\) nên \(2^{27}< 3^{18}\)
Vậy \(2^{27}< 3^{18}\)
Chúc bạn học tốt ~
BT
1
HM
8 tháng 2 2021
ĐIỀU KIỆN : \(x\ge0\)
\(\Rightarrow\hept{\begin{cases}x-2=x\\x-2=-x\end{cases}\Leftrightarrow}\)\(\hept{\begin{cases}0=2\left(vl\right)\\2x=2\end{cases}\Rightarrow x=1\left(tm\right)}\)
Vậy \(x=1\)
TN
0
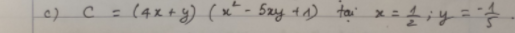
Answer:
\(\frac{x}{3}=\frac{y}{12}=\frac{z}{6}\) \(\Rightarrow\frac{x}{3}=\frac{2y}{24}=\frac{3z}{18}\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{x}{3}=\frac{2y}{24}=\frac{3z}{18}=\frac{x+2y-3z}{3+24-18}=\frac{6}{9}=\frac{2}{3}\)
\(\Rightarrow\frac{x}{3}=\frac{2}{3}\Rightarrow x=2\)
\(\Rightarrow\frac{y}{12}=\frac{2}{3}\Rightarrow y=8\)
\(\Rightarrow\frac{z}{6}=\frac{2}{3}\Rightarrow z=4\)