
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c)\(\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{3}\right)\left(1+\dfrac{1}{4}\right)....\left(1+\dfrac{1}{2020}\right)\left(1+\dfrac{1}{2021}\right)\)
\(=\left(\dfrac{1.2}{1.2}+\dfrac{1}{2}\right)\left(\dfrac{1.3}{1.3}+\dfrac{1}{3}\right)...\left(\dfrac{1.2021}{1.2021}+\dfrac{1}{2021}\right)\)
\(=\dfrac{3}{1.2}\cdot\dfrac{4}{1.3}\cdot\cdot\cdot\cdot\dfrac{2022}{1.2021}\)
\(=\dfrac{3.4.5...2022}{\left(1.1.1....1\right)\left(2.3.4...2021\right)}\)
\(=\)\(\dfrac{3.4.5...2022}{2.3.4...2021}\)
\(=\dfrac{2022}{2}=1011\)
\(d\))\(\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)....\left(1-\dfrac{1}{199}\right)\left(1-\dfrac{1}{200}\right)\)
\(=\left(\dfrac{2}{1.2}-\dfrac{1}{1.2}\right)\left(\dfrac{3}{1.3}-\dfrac{1}{1.3}\right)....\left(\dfrac{200}{1.200}-\dfrac{1}{1.200}\right)\)
\(=\dfrac{1.2.3....199}{\left(1.1.1....1\right).\left(2.3.4....200\right)}\)
\(=\dfrac{1.2.3...199}{2.3.4...200}\)
Nếu mik làm sai mong bạn thông cảm



`4 / 7 xx [-5] / 6 xx 7 / 4 xx 12 / 5`
`= [ 4 xx (-5) xx 7 xx 12 ] / [ 7 xx 6 xx 4 xx 5 ]`
`= [ 4 xx (-5) xx 7 xx 6 xx 2 ] / [ 7 xx 6 xx 4 xx 5 ]`
`= -2`
4/7 × -5/7 × 7/4 ×12/5
=> -10/21 × 42/10
=> -420/210
=> -42/21
Đáp số: -42/21



\(A=\dfrac{1}{2}+\dfrac{2}{4}+\dfrac{3}{8}+...+\dfrac{10}{2^{10}}\)
\(2A=\dfrac{1}{1}+\dfrac{2}{2}+\dfrac{3}{4}+...+\dfrac{10}{2^9}\)
\(2A-A=\left(1+\dfrac{2}{2}+\dfrac{3}{4}+...+\dfrac{10}{2^9}\right)-\left(\dfrac{1}{2}+\dfrac{2}{4}+...+\dfrac{10}{2^{10}}\right)\)
\(A=1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2^9}-\dfrac{10}{2^{10}}\)
\(B=1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2^9}\)
\(2B=2+1+\dfrac{1}{2}+...+\dfrac{1}{2^8}\)
\(2B-B=\left(2+1+\dfrac{1}{2}+...+\dfrac{1}{2^8}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2^9}\right)\)
\(B=2-\dfrac{1}{2^9}\)
Suy ra \(A=B-\dfrac{10}{2^{10}}=2-\dfrac{1}{2^9}-\dfrac{10}{2^{10}}=\dfrac{509}{256}\)

Answer:
\(\dfrac{1}{2}+\dfrac{2}{4}+\dfrac{3}{8}+...+\dfrac{10}{2^{10}}\)
\(=\left(\dfrac{2}{2^0}-\dfrac{3}{2^1}\right)+\left(\dfrac{3}{2^1}-\dfrac{4}{2^2}\right)+\left(\dfrac{4}{2^2}+\dfrac{5}{2^3}\right)+...+\left(\dfrac{11}{2^9}-\dfrac{12}{2^{10}}\right)\)
\(=2-\dfrac{12}{2^{10}}\)
\(=2-\dfrac{3}{256}\)
\(=\dfrac{512}{256}-\dfrac{3}{256}\)
\(=\dfrac{509}{256}\)
*Để làm bài này dễ hơn, bạn áp dụng công thức sau:
\(\dfrac{n}{2^n}=\dfrac{n+1}{2^{n-1}}-\dfrac{n+2}{2^n}\)

\(\Leftrightarrow14-\frac{72}{-\left(8+x\right)}=-23\)
\(\Leftrightarrow37+\frac{72}{8+x}=0\)
\(\Leftrightarrow37\left(8+x\right)+72=0\)
\(\Leftrightarrow296+37x+72=0\)
\(\Leftrightarrow37x=-368\Leftrightarrow x=-\frac{368}{37}\)
 giúp mik bài này với ạ!! mik cảm ơn
giúp mik bài này với ạ!! mik cảm ơn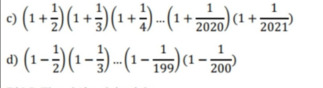

 2 bài này các bạn giúp mik phần d,e,f với
2 bài này các bạn giúp mik phần d,e,f với  còn bài này các bạn giúp mik phần c, h
còn bài này các bạn giúp mik phần c, h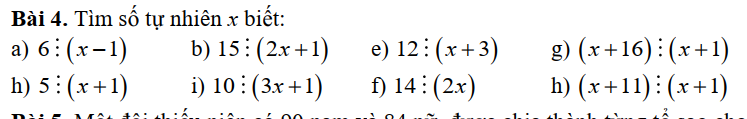 bài này các bạn giúp mik phần g, h, i
bài này các bạn giúp mik phần g, h, i các bạn giúp mik hết luôn hai bài này nhé, mik đang cần cực kì gấp
các bạn giúp mik hết luôn hai bài này nhé, mik đang cần cực kì gấp


b) \(B=\frac{4}{1.6}+\frac{4}{6.11}+\frac{4}{11.16}+...+\frac{4}{96.101}\)
\(=\frac{4}{5}\left(\frac{5}{1.6}+\frac{5}{6.11}+\frac{5}{11.16}+...+\frac{5}{96.101}\right)\)
\(=\frac{4}{5}\left(1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+\frac{1}{11}-\frac{1}{16}+...+\frac{1}{96}-\frac{1}{101}\right)\)
\(=\frac{4}{5}\left(1-\frac{1}{101}\right)\)
\(=\frac{80}{101}\)