
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Ta có
\(\left|x-1,7\right|=2,3\\ \Rightarrow\left[{}\begin{matrix}x-1,7=2.3\\x-1.7=-2,3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=4\\x=-0,6\end{matrix}\right.\)
Vậy....
b, Ta có :
\(\left|x+\dfrac{3}{4}\right|-\dfrac{1}{3}=0\\ \Rightarrow\left|x+\dfrac{3}{4}\right|=\dfrac{1}{3}\\ \Rightarrow\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{3}\\x+\dfrac{3}{4}=-\dfrac{1}{3}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{5}{12}\\x=-\dfrac{13}{12}\end{matrix}\right.\)
Vậy...

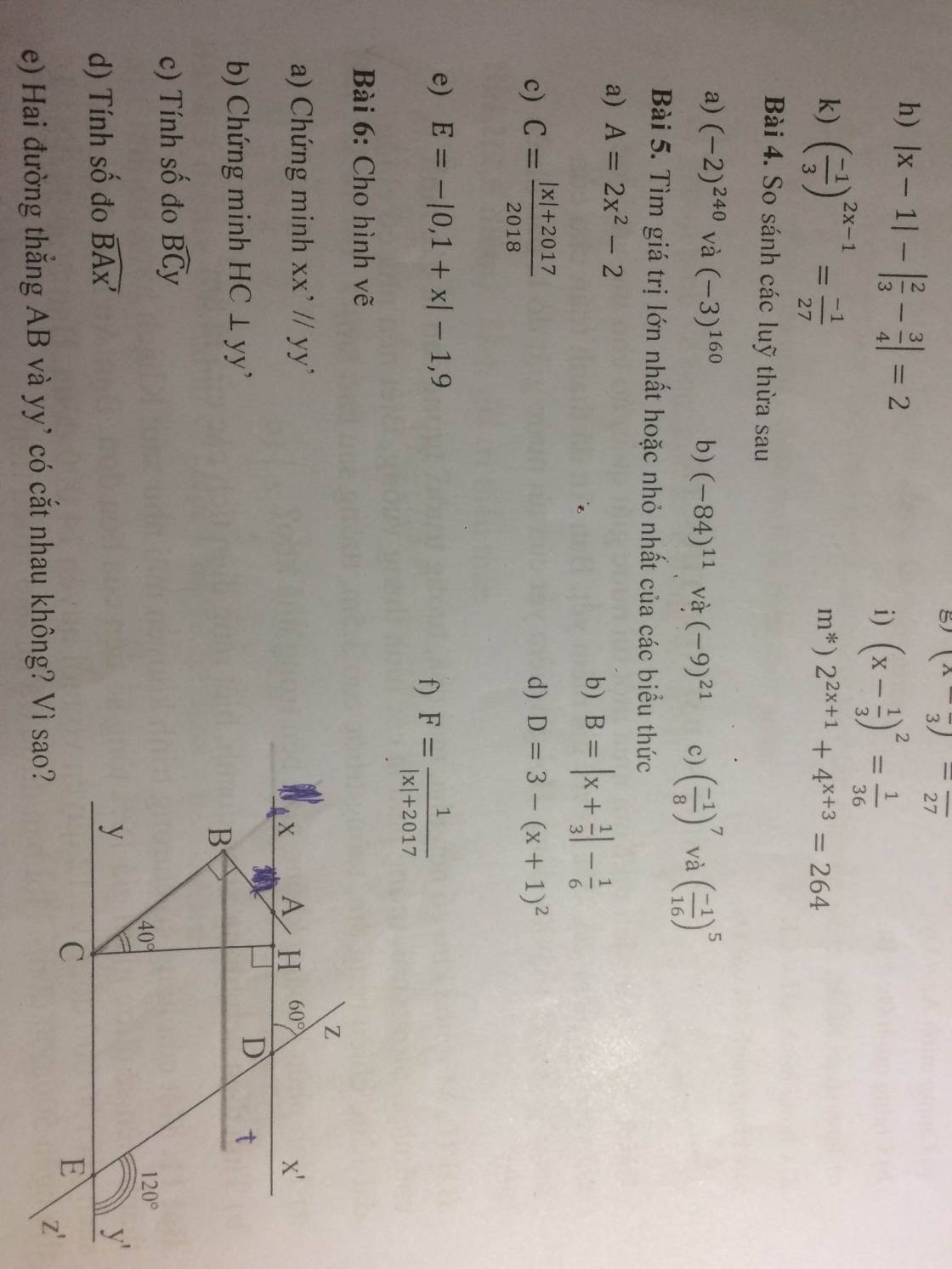
a) ∠CEz + ∠zEy' = 180⁰ (kề bù)
⇒ ∠CEz = 180⁰ - ∠zEy'
= 180⁰ - 120⁰
= 60⁰
⇒ ∠CEz = ∠xDz = 60⁰
Mà ∠CEz và ∠xDz là hai góc đồng vị
⇒ xx' // yy'
b) Do HC ⊥ xx' (gt)
xx' // yy' (cmt)
⇒ HC ⊥ yy'
c) Do HC ⊥ yy' (cmt)
⇒ ∠HCy = 90⁰
⇒ ∠BCy = ∠HCy - ∠BCH
= 90⁰ - 40⁰
= 50⁰
c) Vẽ tia Bt // xx'//yy'
⇒ ∠CBt = ∠BCy = 50⁰ (so le trong)
⇒ ∠ABt = ∠ABC - ∠CBt
= 90⁰ - 50⁰
= 40⁰
Do Bt // xx'
⇒ ∠xAB = ∠ABt = 40⁰ (so le trong)
Ta có:
∠BAx' + ∠xAB = 180⁰ (kề bù)
⇒ ∠BAx' = 180⁰ - ∠xAB
= 180⁰ - 40⁰
= 140⁰
e) Do AB cắt tia Bt tại B
Mà Bt // yy'
⇒ AB cắt yy'


Bài 2.
a. góc xAB + góc ABy = 45+135 = 180 (độ)
--> góc xAB và ABy là hai góc trong cùng phía bù nhau
--> Ax // By (đpcm)
b. góc CBy =360 - 75 -135 = 150 (độ)
--> góc CBy + góc CBz = 150 +30 =180 (độ)
--> góc CBy và CBz là hai góc trong cùng phía bù nhau
--> By//Cz (đpcm)

Ta có:
-7/13=-70/130=-7.10/13.10
-4/13=-40/130=-4.10/13.10
=>p/s đó là a.13/10.13
=>-7.10<a.13<-4.10
=>a=-4;-5
Vậy p/s đó là:-4/10 và -5/10

Bài 3:
a) \(\Rightarrow\dfrac{2}{15}x=-\dfrac{11}{15}\Rightarrow x=-\dfrac{11}{2}\)
b) \(\Rightarrow\left|x+\dfrac{1}{3}\right|=5\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{1}{3}=5\\x+\dfrac{1}{3}=-5\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{14}{3}\\x=-\dfrac{16}{3}\end{matrix}\right.\)
Bài 4:
Áp dụng t/c dtsbn:
\(\dfrac{a}{11}=\dfrac{b}{9}=\dfrac{c}{12}=\dfrac{a-b+c}{11-9+12}=\dfrac{-28}{14}=-2\)
\(\Rightarrow\left\{{}\begin{matrix}a=\left(-2\right).11=-22\\b=\left(-2\right).9=-18\\c=\left(-2\right).12=-24\end{matrix}\right.\)

\(\frac{x+1}{2009}+\frac{x+2}{2008}+\frac{x+3}{2007}=\frac{x+10}{2000}+\frac{x+11}{1999}+\frac{x+12}{1998}.\)
\(\frac{x+1}{2009}+1+\frac{x+2}{2008}+1+\frac{x+3}{2007}+1=\frac{x+10}{2000}+1+\frac{x+11}{1999}+1+\frac{x+12}{1998}+1.\)(cộng 2 vế cho 3)
\(\frac{x+1}{2009}+\frac{2009}{2009}+\frac{x+2}{2008}+\frac{2008}{2008}+\frac{x+3}{2007}+\frac{2007}{2007}=\frac{x+10}{2000}+\frac{2000}{2000}+\frac{x+11}{1999}+\frac{1999}{1999}+\frac{x+12}{1998}+\frac{1998}{1998}.\)
\(\frac{x+2010}{2009}+\frac{x+2010}{2008}+\frac{x+2010}{2007}=\frac{x+2010}{2000}+\frac{x+2010}{1999}+\frac{x+2010}{1998}.\)
\(\frac{x+2010}{2009}+\frac{x+2010}{2008}+\frac{x+2010}{2007}-\frac{x+2010}{2000}-\frac{x+2010}{1999}-\frac{x+2010}{1998}=0\)
x+2010=0
x=-2010
\(\frac{x+1}{2009}+\frac{x+2}{2008}+\frac{x+3}{2007}=\frac{x+10}{2000}+\frac{x+11}{1999}+\frac{x+12}{1998}\)
\(\Leftrightarrow\left(1+\frac{x+1}{2009}\right)+\left(1+\frac{x+2}{2008}\right)+\left(1+\frac{x+3}{2007}\right)\)
\(=\left(1+\frac{x+10}{2000}\right)+\left(1+\frac{x+11}{1999}\right)+\left(1+\frac{x+12}{1998}\right)\)
\(\Leftrightarrow\frac{x+2010}{2009}+\frac{x+2010}{2008}+\frac{x+2010}{2007}=\frac{x+2010}{2000}+\frac{x+2010}{1999}+\frac{x=2010}{1998}\)
\(\Leftrightarrow\frac{x+2010}{2009}+\frac{x+2010}{2008}+\frac{x+2010}{2007}-\frac{x+2010}{2000}-\frac{x+2010}{1999}-\frac{x+2010}{1998}\)
\(=0\)
\(\Leftrightarrow\left(x+2010\right)\left(\frac{1}{2009}+\frac{1}{2008}+\frac{1}{2007}-\frac{1}{2000}-\frac{1}{1999}-\frac{1}{1998}\right)=0\)
\(\Leftrightarrow x+2010=0\)
\(\Leftrightarrow x=-2010\)

minh co gang lam tung buoc nho cho ban hieu.
\(4-\left(x-\frac{1}{2}\right)-3\left(5-x\right)=0\)
{nhan pp pha ngoac
\(4-x+\frac{1}{2}-3.5+3.x=0\)
{gom cac so hang, hang so chuyen ben tay phai}
\(\left(3x-x\right)=3.5-4-\frac{1}{2}=15-4-\frac{1}{2}=11-\frac{1}{2}=\frac{21}{2}\)
\(2x=\frac{21}{2}\Rightarrow x=\frac{21}{2}:\frac{2}{1}=\frac{21}{2}.\frac{1}{2}=\frac{21}{4}\)
\(x=\frac{21}{4}\)

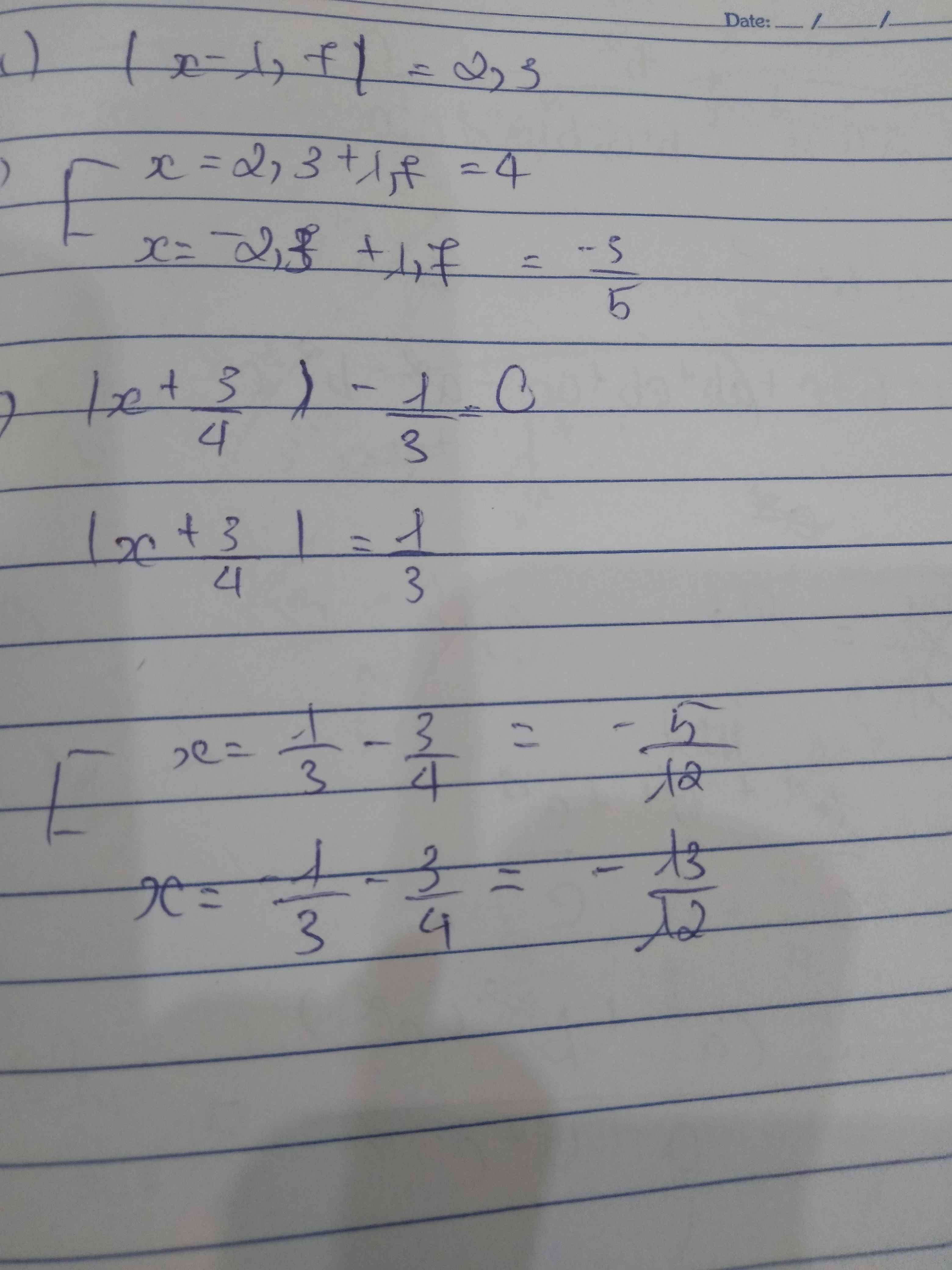






a)+Gọi số đo các góc đó lần lượt là x;y;z(độ)
Điều kiện x;y;z >0
+Vì tổng 3 góc của tam giác bằng 180* và các góc A,B,C tương ứng tỉ lệ với 1;2;2 nên ta có:
x/1=y/2=z/3 và x+y+z=180*
+ Ap dụng tính chất của dãy tỉ số bằng nhau ta có:
x/1=y/2=z/3=x+y+z/1+2+3=180*/5*=36
+Do đó:
x/1=36=>x=36.1=36*(TMĐK)
y/2=36=>y=36.2=72*(TMĐK)
z/3=36=>z=36.3=108*(TMĐK)
Vậy số đo các góc lần lượt là 36*;72*;108* (* là độ nhé)
b thì mk ko biết nhé bạn
Chúc bạn học giỏi