
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


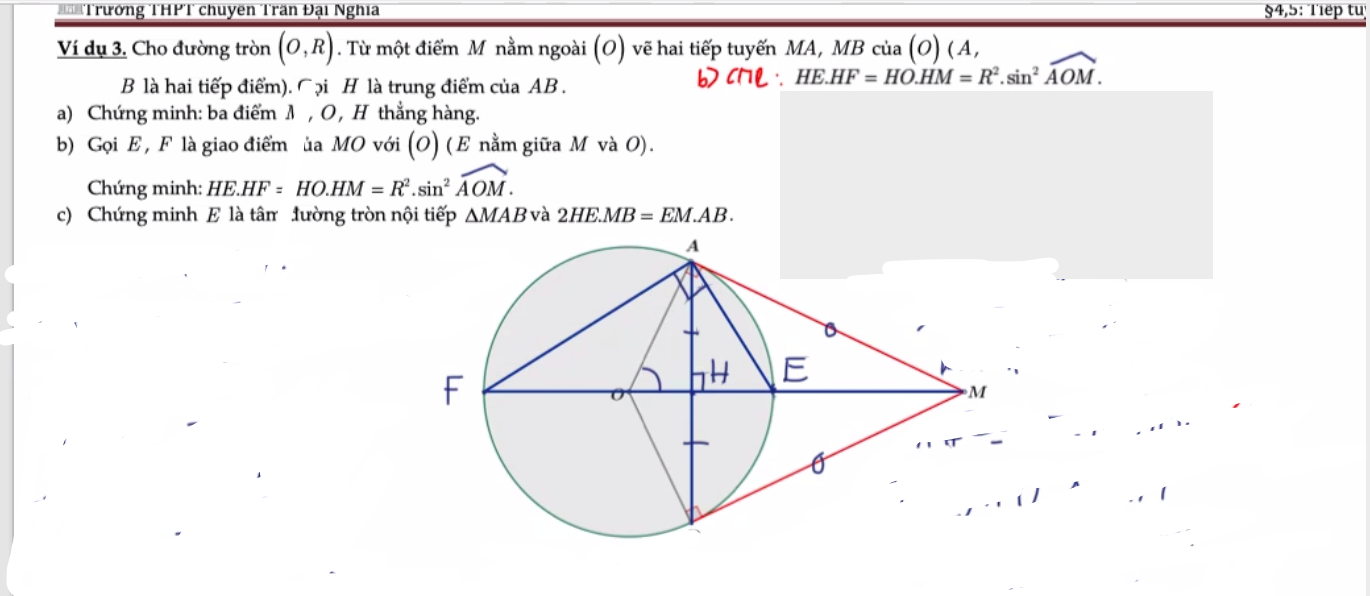
Theo t/c 2 tiếp tuyến \(AM=BM\Rightarrow\Delta ABM\) cân tại M
\(\Rightarrow MH\) là trung tuyến, đường cao, trung trực AB đồng thời là phân giác \(\widehat{AMB}\)
\(\Rightarrow AE=BE\Rightarrow\Delta ABE\) cân tại E
\(\Rightarrow\widehat{ABE}=\widehat{BAE}\)
Mà \(\widehat{ABE}=\widehat{MAE}\) (cùng chắn cung AE)
\(\Rightarrow\widehat{BAE}=\widehat{MAE}\Rightarrow AE\) là phân giác \(\widehat{BAM}\)
\(\Rightarrow\) E là giao điểm 2 đường phân giác trong của tam giác ABM hay E là tâm đường tròn nội tiếp tam giác
Theo định lý phân giác (trong tam giác AHM)
\(\dfrac{HE}{AH}=\dfrac{ME}{AM}\Rightarrow ME.AH=HE.AM\Rightarrow ME.\dfrac{AB}{2}=HE.BM\Rightarrow2HE.BM=ME.AB\)




a) Bảng phân bố tần số (về tuổi thọ bóng đèn điện) có thể viết dưới dạng như sau:

Số trung bình về tuổi thọ của bóng đèn trong bảng phân bố trên là:
.(3x1150 + 6x1160 + 12x1170 + 6x1180 + 3x1190)
= 1170.
b) Số trung bình về chiều dài lá cây dương xỉ trong bài tập 2 trong là:
.(8x15 + 18x25 + 24x35 + 10x45) = 31 (cm).














 giúp e với,sắp thi r
giúp e với,sắp thi r

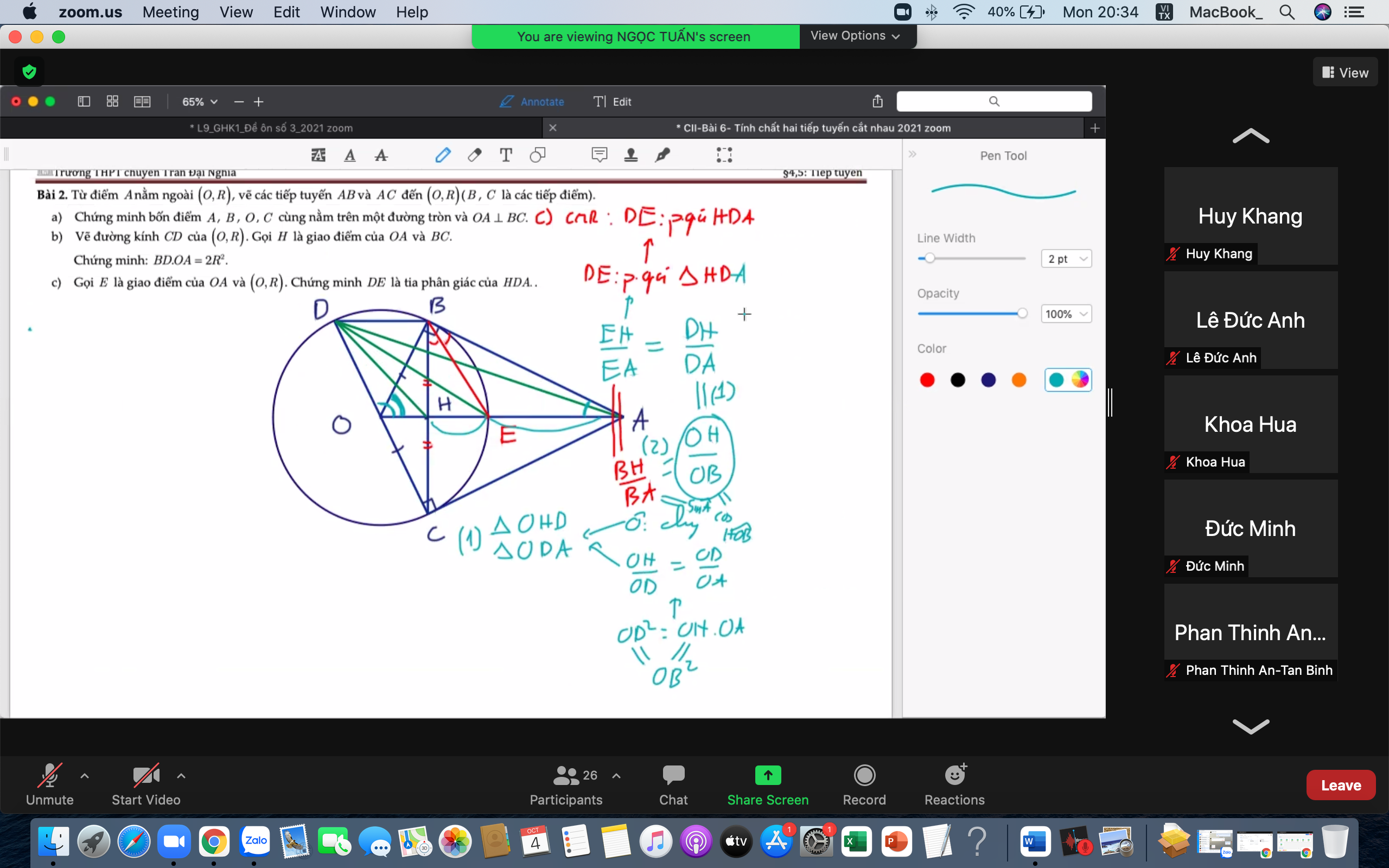
Ta có: \(\widehat{DBC}=90^0\) (nt chắn nửa đường tròn)
\(\Rightarrow BD||OA\) (cùng vuông góc BC)
\(\Rightarrow\widehat{BDE}=\widehat{DEO}\) (slt)
Mà \(\widehat{DEO}=\widehat{ODE}\) (OD=OE=R nên tam giác ODE cân tại O)
\(\Rightarrow\widehat{ODE}=\widehat{BDE}\) (1)
Lại có OH là đường trung bình tam giác BCD (đi qua 2 trung điểm)
\(\Rightarrow BD=2OH\)
Theo câu b: \(BD.OA=2R^2=2OD^2\Rightarrow2OH.OA=2OD^2\)
\(\Rightarrow\dfrac{OH}{OD}=\dfrac{OD}{OA}\)
Hai tam giác ODH và OAD có: \(\left\{{}\begin{matrix}\widehat{O}\text{ chung}\\\dfrac{OH}{OD}=\dfrac{OD}{OA}\end{matrix}\right.\)
\(\Rightarrow\Delta ODH\sim\Delta OAD\Rightarrow\widehat{ODH}=\widehat{OAD}\)
Mà \(\widehat{OAD}=\widehat{BDA}\) (so le trong) (2)
(1);(2) \(\Rightarrow\widehat{HDE}=\widehat{ADE}\) hay DE là phân giác \(\widehat{HDA}\)