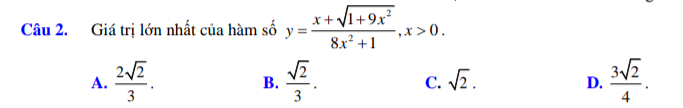Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài này chắc khỏi đạo hàm:
\(y=\dfrac{3\sqrt{2}.2.\dfrac{\sqrt{2}}{12}x+\dfrac{\sqrt{2}}{3}.2.\dfrac{3\sqrt{2}}{4}\sqrt{1+9x^2}}{8x^2+1}\le\dfrac{3\sqrt{2}\left(\dfrac{1}{72}+x^2\right)+\dfrac{\sqrt{2}}{3}\left(\dfrac{9}{8}+1+9x^2\right)}{8x^2+1}\)
\(y\le\dfrac{\sqrt{2}\left(6x^2+\dfrac{3}{4}\right)}{8x^2+1}=\dfrac{3\sqrt{2}}{4}.\dfrac{8x^2+1}{8x^2+1}=\dfrac{3\sqrt{2}}{4}\)


Theo giả thiết, ta có:
\left( {\widehat {SC,\left( {ABC} \right)}} \right) = \widehat {SCA} = {30^^\circ } \Rightarrow SA = AC\tan {30^^\circ } = \frac{{a\sqrt 3 }}{3}
Vậy thể tích khối chóp S.ABC là:

\(y'=\left(2m+1\right)\cos x+3-m\)
Hàm số đã cho đồng biến trên R \(\Leftrightarrow y'\ge0,\forall x\in R\)
\(\Leftrightarrow\left(2m+1\right)\cos x\le m-3\) (1)
*TH: \(2m+1< 0\Leftrightarrow m< \frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\ge\frac{m-3}{2m+1}\) (không thoả với mọi x)
*TH: \(2m+1>0\Leftrightarrow m>\frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\le\frac{m-3}{2m+1}\) (2)
(2) đúng với mọi x khi và chỉ khi \(\left|\frac{m-3}{2m+1}\right|>1\Leftrightarrow\left[\begin{array}{nghiempt}m< -4\\m>\frac{2}{3}\end{array}\right.\)
kết hợp \(m>\frac{-1}{2}\) ta có m > 3/2 là giá trị cần tìm


Cắt mỗi quả thành 8 phần bằng nhau, như vậy 7 quả sẽ được 56 phần. Sau đó chia đều cho 8 người, mỗi người được 7 phần như nhau.
7 quả táo chia cho mỗi người thì mỗi người đc 7/8 số táo
chia mỗi quả táo thành 8 miếng
Suy ra mỗi người 7 miếng