Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

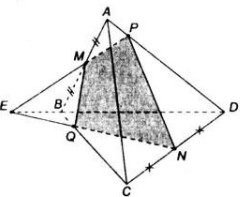
a) Gọi \(N=DK\cap AC;M=DJ\cap BC\).
Ta có \(\left(DJK\right)\cap\left(ABC\right)=MN\Rightarrow MN\subset\left(ABC\right)\)
Vì \(L=\left(ABC\right)\cap JK\) nên dễ thấy \(L=JK\cap MN\)


a) Gọi N = DK ∩ AC; M = DJ ∩ BC.
Ta có (DJK) ∩ (ABC) = MN ⇒ MN ⊂ (ABC).
Vì L = (ABC) ∩ JK nên dễ thấy L = JK ∩ MN.
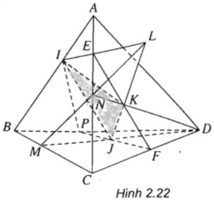
b) Ta có I là một điểm chung của (ABC) và (IJK).
Mặt khác vì L = MN ∩ JK mà MN ⊂ (ABC) và JK ⊂ (IJK) nên L là điểm chung thứ hai của (ABC) và (IJK), suy ra (IJK) ∩ (ABC) = IL.
Gọi E = IL ∩ AC; F = EK ∩ CD. Lí luận tương tự ta có EF = (IJK) ∩ (ACD).
Nối FJ cắt BD tại P; P là một giao điểm (IJK) và (BCD).
Ta có PF = (IJK) ∩ (BCD) Và IP = (ABD) ∩ (IJK)

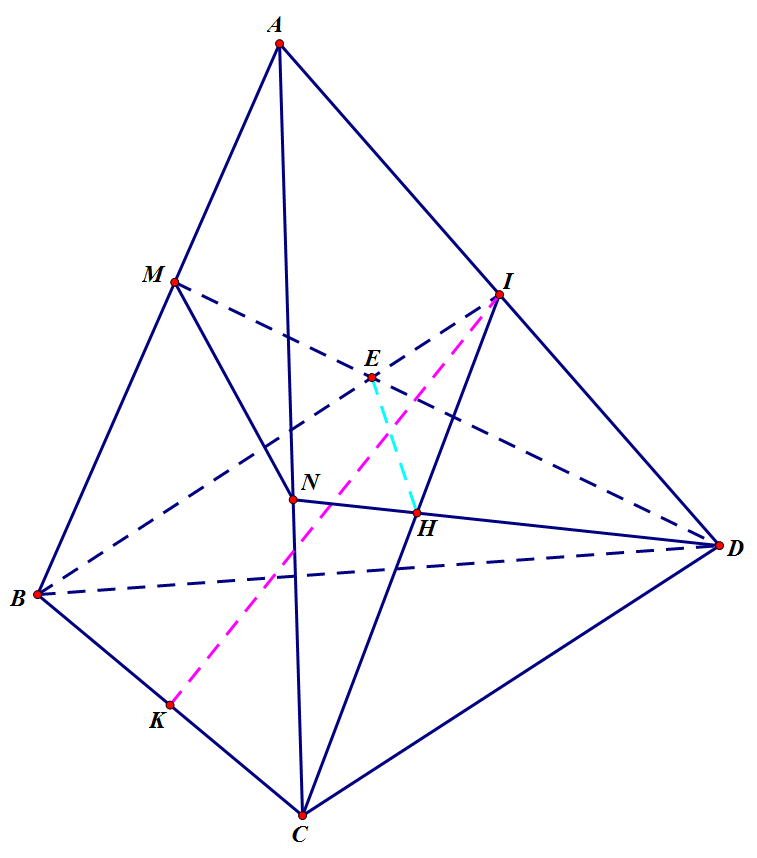
a,Hiển nhiên : K ∈ (KAD), mà K ∈ BC nên K ∈ (BCD)
Hiển nhiên : D ∈ (KAD) và D ∈ (BCD)
⇒ (KAD) \(\cap\) (BCD) = DK
b, Hiển nhiên : K ∈ (KAD), mà K ∈ BC nên K ∈ (IBC)
Hiển nhiên I ∈ (IBC), mà I ∈ AD nên I ∈ (KAD)
⇒ (KAD) \(\cap\) (BCI) = IK
c, Trong (ABD) gọi E là giao điểm của BI và DM
⇒ \(\left\{{}\begin{matrix}E\in\left(IBC\right)\\E\in\left(DMN\right)\end{matrix}\right.\)
Trong (ACD) gọi F là giao điểm của CI và DN
⇒ \(\left\{{}\begin{matrix}F\in\left(IBC\right)\\F\in\left(DMN\right)\end{matrix}\right.\)
Vậy (DMN) \(\cap\) (IBC) = EF

 phần c là hỏi về thiết diện của tứ diện ABCD cắt bởi (AG1G2) đk bn ???🤔
phần c là hỏi về thiết diện của tứ diện ABCD cắt bởi (AG1G2) đk bn ???🤔

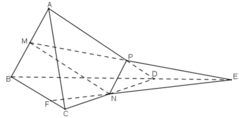
a) Trong mp(ABD): MP không song song với BD nên MP ∩ BD = E.
E ∈ MP ⇒ E ∈ (PMN)
E ∈ BD ⇒ E ∈ (BCD)
⇒ E ∈ (PMN) ∩ (BCD)
Dễ dàng nhận thấy N ∈ (PMN) ∩ (BCD)
⇒ EN = (PMN) ∩ (BCD)
b) Trong mp(BCD) : gọi giao điểm EN và BC là F.
F ∈ EN, mà EN ⊂ (PMN) ⇒ F ∈ (PMN)
⇒ F = (PMN) ∩ BC.

Câu b đề bài thiếu, tìm giao tuyến của mặt nào và (ABD) vậy em?