
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



71.
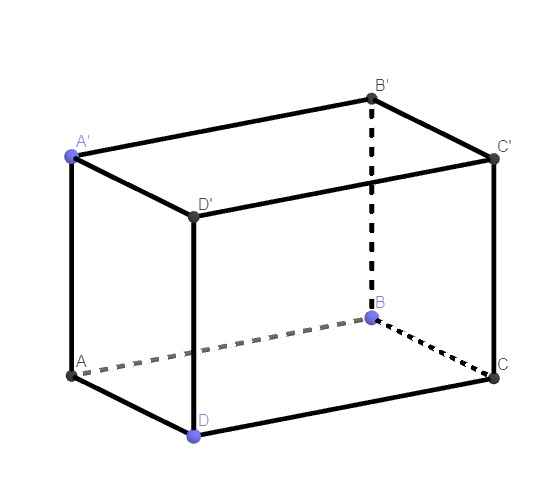
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)

Bài này xài L'Hopital đi, chứ tách biểu thức chắc đến sáng mai :D
\(\lim\limits_{x\rightarrow1}\dfrac{x^{2020}-2020x+2019}{\left(x-1\right)^2}=\lim\limits_{x\rightarrow1}\dfrac{2020x^{2019}-2020}{2\left(x-1\right)}=\lim\limits_{x\rightarrow1}\dfrac{2019.2020.x^{2018}}{2}=1010.2019\)
Hàm liên tục tại \(x=1\) khi: \(m+1=1010.2019\Rightarrow m=1010.2019-1\)

Do n lẻ, đặt \(n=2m+1\)
\(\Rightarrow S=C_{2m+1}^1+C_{2m+1}^2+...+C_{2m+1}^m\)
Áp dụng đẳng thức: \(C_n^k=C_n^{n-k}\)
\(\Rightarrow S=C_{2m+1}^{2m}+C_{2m+1}^{2m-1}+...+C_{2m+1}^{m+1}\)
\(\Rightarrow2S=S+S=C_{2m+1}^1+C_{2m+1}^2+...+C_{2m+1}^{2m}\)
\(=C_{2m+1}^0+C_{2m+1}^1+...+C_{2m+1}^{2m+1}-\left(C_{2m+1}^0+C_{2m+1}^{2m+1}\right)\)
\(=2^{2m+1}-2\)
\(\Rightarrow S=2^{2m}-1\) luôn lẻ (đpcm)


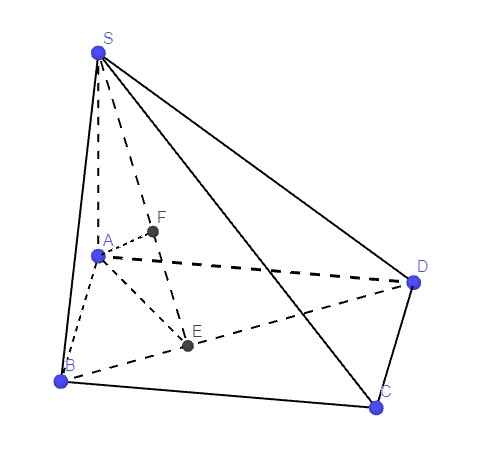
Kẻ \(AE\perp BD\) , \(AF\perp SE\Rightarrow AF\perp\left(SBD\right)\)
Dễ dàng chứng minh \(AD\perp\left(SAB\right)\) ; \(AB\perp\left(SAD\right)\)
Từ đó ta có: \(\alpha=\widehat{FAD}\) ; \(\beta=\widehat{FAB}\) ; \(\gamma=\widehat{FAS}\)
\(\dfrac{1}{AF^2}=\dfrac{1}{SA^2}+\dfrac{1}{AE^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}+\dfrac{1}{AD^2}=\dfrac{2}{a^2}+\dfrac{1}{b^2}=\dfrac{a^2+2b^2}{a^2b^2}\)
\(\Rightarrow AF=\dfrac{ab}{\sqrt{a^2+2b^2}}\)
\(\Rightarrow T=cos\alpha+cos\beta+cos\gamma=\dfrac{AF}{AD}+\dfrac{AF}{AB}+\dfrac{AF}{AS}=\dfrac{ab}{\sqrt{a^2+2b^2}}\left(\dfrac{2}{a}+\dfrac{1}{b}\right)\)
\(\Rightarrow T=\dfrac{\sqrt{3}ab}{\sqrt{\left(1+2\right)\left(a^2+2b^2\right)}}\left(\dfrac{a+2b}{ab}\right)\le\dfrac{\sqrt{3}ab}{a+2b}\left(\dfrac{a+2b}{ab}\right)=\sqrt{3}\)
Dấu "=" xảy ra khi và chỉ khi \(a=b\)

Trên thực tế điểm P nằm ở đâu trên SC đều không quan trọng
Ta có: \(\overrightarrow{AI}=\dfrac{1}{3}\overrightarrow{AB}\Rightarrow\dfrac{AI}{AB}=\dfrac{1}{3}\)
\(\overrightarrow{DJ}=\dfrac{2}{3}\overrightarrow{DA}\Rightarrow\overrightarrow{AJ}=\dfrac{1}{3}\overrightarrow{AD}\Rightarrow\dfrac{AJ}{AD}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{AI}{AB}=\dfrac{AJ}{AD}\Rightarrow IJ||BD\) (Talet đảo) (1)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp AP\) (2)
(1);(2) \(\Rightarrow IJ\perp AP\) hay góc giữa 2 đường thẳng bằng \(\dfrac{\pi}{2}\)

\(\dfrac{1}{u_{n+1}}=\dfrac{1}{u_n}+nu_n\)
Đặt \(v_n=\dfrac{1}{u_n}\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{2022}\\v_{n+1}=v_n+\dfrac{n}{v_n}\end{matrix}\right.\) và \(\left\{\dfrac{1}{nu_n}\right\}=\left\{\dfrac{v_n}{n}\right\}\)
Ta sẽ chứng minh \(v_n\ge n\) với \(n>1\)
Với \(n=2\Rightarrow v_2=v_1+2022>2\) (đúng)
Giả sử điều đó đúng với \(n=k>1\) hay \(v_k\ge k\)
Ta cần chứng minh \(v_{k+1}\ge k+1\)
Thật vậy, do \(v_k\ge k\), đặt \(v_k=k+\alpha\) với \(\alpha\ge0\)
Khi đó: \(v_{k+1}=v_k+\dfrac{k}{v_k}=k+\alpha+\dfrac{k}{k+\alpha}=k+\dfrac{k\alpha+\alpha^2+k}{k+\alpha}\ge k+\dfrac{\alpha+k}{k+\alpha}=k+1\) (đpcm)
Tương tự, ta quy nạp chứng minh được \(v_n\le n+v_2\) với \(n>1\) (do \(v_2\) số xấu nên ko ghi)
Kiểm tra với \(n=2\Rightarrow v_2\le2+v_2\) (đúng)
Giả sử \(v_k\le k+v_2\)
\(\Rightarrow v_{k+1}=v_k+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{k}=k+1+v_2\) (đpcm)
\(\Rightarrow n\le v_n\le n+v_2\) \(\Rightarrow1\le\dfrac{v_n}{n}\le\dfrac{n+v_2}{n}\)
Sử dụng định lý kẹp, dễ dàng suy ra \(\lim\left\{\dfrac{v_n}{n}\right\}=1\)





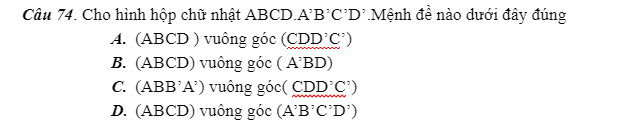
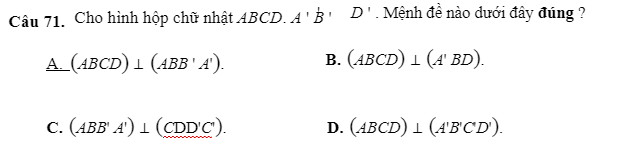
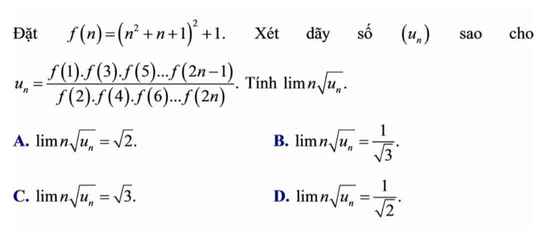
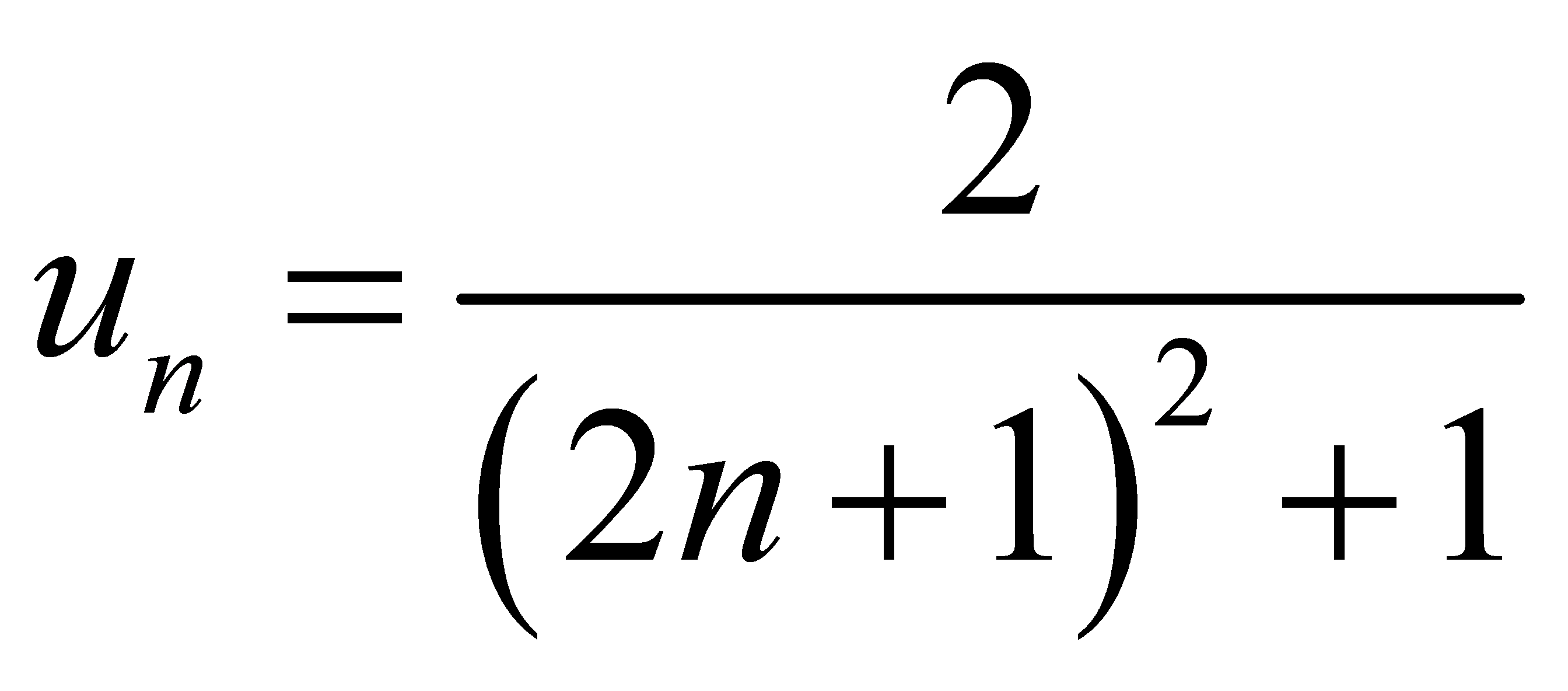
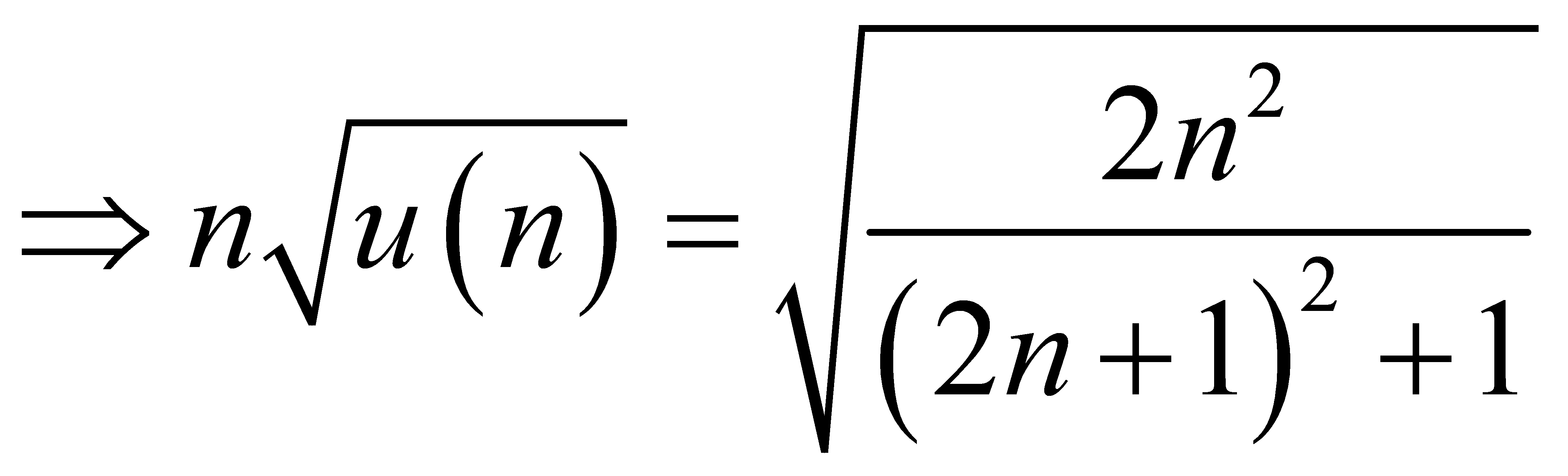 .
. 
 .
. 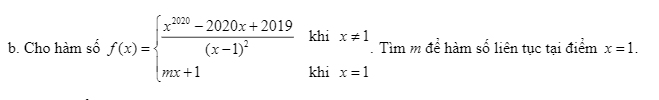


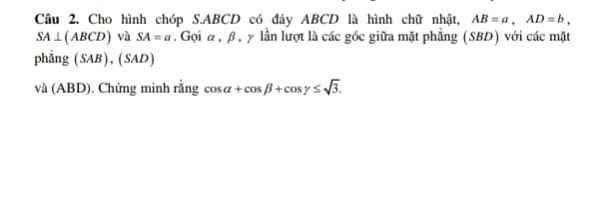

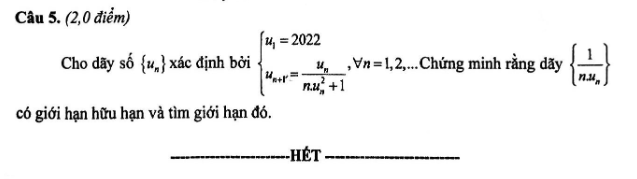 giúp em với em cảm ơn nhiều ạ
giúp em với em cảm ơn nhiều ạ