
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


6:
\(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{150}=\left(3^2\right)^{75}=9^{75}\)
mà 8<9
nên \(2^{225}< 3^{150}\)
4: \(\left|5x+3\right|>=0\forall x\)
=>\(-\left|5x+3\right|< =0\forall x\)
=>\(-\left|5x+3\right|+5< =5\forall x\)
Dấu = xảy ra khi 5x+3=0
=>x=-3/5
1:
\(\left(2x+1\right)^4>=0\)
=>\(\left(2x+1\right)^4+2>=2\)
=>\(M=\dfrac{3}{\left(2x+1\right)^4+2}< =\dfrac{3}{2}\)
Dấu = xảy ra khi 2x+1=0
=>x=-1/2

a) Ta có:
\(\widehat{yOu}+\widehat{xOy}=180^o\) (kề bù)
\(\Rightarrow\widehat{yOu}=180^o-\widehat{xOy}\)
\(\Rightarrow\widehat{yOu}=180^o-60^o=120^o\)
Mà: \(\widehat{xOt}+\widehat{tOu}=180^o\) (kề bù)
\(\Rightarrow\widehat{xOt}=180^o-\widehat{tOu}\)
\(\Rightarrow\widehat{xOt}=180^o-30^o=150^o\)
b) Ta có:
\(\widehat{xOy}+\widehat{yOt}+\widehat{tOu}=\widehat{xOu}\)
\(\Rightarrow\widehat{yOt}=\widehat{xOu}-\widehat{xOy}-\widehat{tOu}\)
\(\Rightarrow\widehat{yOt}=180^o-60^o-30^o\)
\(\Rightarrow\widehat{yOt}=90^o\)

1: \(\sqrt{11}\) là số vô tỉ
2:
a: 4,9(18)=4,91818...
mà 4,91818<4,928
nên 4,9(18)<4,928
b: 4,315<4,318
=>-4,315>-4,318
=>-4,315...>-4,318...
c: \(\sqrt{3}=\sqrt{\dfrac{6}{2}}< \sqrt{\dfrac{7}{2}}\)
3:
a: \(6=\sqrt{3};-1,7=-\sqrt{2,89}\)
0<2,89<3
=>\(0< \sqrt{2,89}< \sqrt{3}\)
=>\(-\sqrt{3}< -\sqrt{2,89}< 0\)
0<35<36<47
=>\(0< \sqrt{35}< \sqrt{36}< \sqrt{47}\)
=>\(-\sqrt{3}< -\sqrt{2,89}< 0< \sqrt{35}< \sqrt{36}< \sqrt{47}\)
=>\(-\sqrt{3}< -\sqrt{2,89}< 0< \sqrt{35}< 6< \sqrt{47}\)
b: \(-\sqrt{2\dfrac{1}{3}}=-\sqrt{2,\left(3\right)}\)
\(-1,5=-\sqrt{2,25}\)
2,25<2,3<2,(3)
=>\(\sqrt{2.25}< \sqrt{2.3}< \sqrt{2.\left(3\right)}\)
=>\(0>-1.5>-\sqrt{2.3}>-\sqrt{2\dfrac{1}{3}}\)
\(0< \sqrt{5\dfrac{1}{6}}=\sqrt{5,1\left(6\right)}< \sqrt{5,3}\)
=>\(\sqrt{5.3}>\sqrt{5\dfrac{1}{6}}>0>-1.5>-\sqrt{2.3}>-\sqrt{2\dfrac{1}{3}}\)

\(c,-\dfrac{8}{13}+\left(-\dfrac{7}{5}-x\right)=-\dfrac{1}{2}\\ -\dfrac{7}{5}-x=-\dfrac{1}{2}-\dfrac{8}{13}\\ -\dfrac{7}{5}-x=-\dfrac{29}{26}\\ x=-\dfrac{7}{5}-\left(-\dfrac{29}{26}\right)=-\dfrac{37}{130}\\ d,-1\dfrac{1}{7}-\left[-\dfrac{5}{3}+\left(x-\dfrac{7}{3}\right)\right]=-\dfrac{4}{21}\\ -\dfrac{8}{7}-\left[-\dfrac{5}{3}+\left(x-\dfrac{7}{3}\right)\right]=-\dfrac{4}{21}\\ -\dfrac{5}{3}+\left(x-\dfrac{7}{3}\right)=-\dfrac{8}{7}-\left(-\dfrac{4}{21}\right)\\ -\dfrac{5}{3}+\left(x-\dfrac{7}{3}\right)=-\dfrac{20}{21}\\ x-\dfrac{7}{3}=-\dfrac{20}{21}-\left(-\dfrac{5}{3}\right)\\ x-\dfrac{7}{3}=\dfrac{5}{7}\\ x=\dfrac{5}{7}+\dfrac{7}{3}=\dfrac{64}{21}\\ e,-\dfrac{2}{3}-x:\dfrac{1}{2}=\dfrac{2}{5}\\ x:\dfrac{1}{2}=-\dfrac{2}{3}-\dfrac{2}{5}\\ x:\dfrac{1}{2}=-\dfrac{16}{15}\\ x=-\dfrac{16}{15}\times\dfrac{1}{2}=-\dfrac{8}{15}\)
c: -8/13+(-7/5-x)=-1/2
=>x+7/5+8/13=1/2
=>x=1/2-7/5-8/13=-197/130
d: \(\Leftrightarrow-\dfrac{8}{7}+\dfrac{5}{3}-\left(x-\dfrac{7}{3}\right)=\dfrac{-4}{21}\)
=>\(x-\dfrac{7}{3}=\dfrac{-8}{7}+\dfrac{5}{3}+\dfrac{4}{21}=\dfrac{-24+35+4}{21}=\dfrac{18}{21}=\dfrac{6}{7}\)
=>x=6/7+7/3=18/21+49/21=67/21
e: =>x:1/2=-2/3-2/5=-16/15
=>x=-16/15*1/2=-8/15
f: =>-8/5*x=-1/3+4/9=1/9
=>x=-1/9:8/5=-1/9*5/8=-5/72
g: =>-4/5x-1/4+x=-13/3
=>1/5x=-13/3+1/4=-52/12+3/12=-49/12
=>x=-49/12*5=-245/12
h: =>12/7:x-1/2=0 hoặc 2/5x-3/2=0
=>12/7:x=1/2 hoặc 2/5x=3/2
=>x=12/7:1/2=24/7 hoặc x=3/2:2/5=3/2*5/2=15/4

Bài 16
a) \(A=\dfrac{n+1}{n+2}\)
Gọi ƯCLN(n+1;n+2) là x ( \(x\in N\) *)
\(\Rightarrow\) \(\left\{{}\begin{matrix}\left(n+1\right)⋮x\\\left(n+2\right)⋮x\end{matrix}\right.\)
\(\Rightarrow\) \(\left(n+2\right)-\left(n+1\right)\) \(⋮x\)
\(\Rightarrow\) \(1\) \(⋮x\)
\(\Rightarrow\) x = 1 \(\Rightarrow\) ƯCLN(n+1;n+2)=1
Vậy A là phân số tối giản ( vì có ƯCLN = 1)
b) \(B=\dfrac{n+1}{3n+4}\)
Gọi ƯCLN(n+1;3n+4) là d ( \(d\in N\) *)
\(\Rightarrow\) \(\left\{{}\begin{matrix}n+1⋮d\\3n+4⋮d\end{matrix}\right.\)
\(\Rightarrow\) \(\left\{{}\begin{matrix}3n+3⋮d\\3n+4⋮d\end{matrix}\right.\)
\(\Rightarrow\) (3n+4)-(3n+3) chia hết cho d
\(\Rightarrow\) \(1⋮d\)
\(\Rightarrow\) d =1
Vậy B là phân số tối giản.
Mấy phần kia tương tự
c: Gọi d=ƯCLN(3n+2;5n+3)
=>3n+2 chia hết cho d và 5n+3 chia hết cho d
=>15n+10 chia hết cho d và 15n+9 chia hết cho d
=>1 chia hết cho d
=>ƯCLN(3n+2;5n+3)=1
=>PSTG
d: Gọi d=ƯCLN(12n+1;30n+2)
=>12n+1 và 30n+2 đều chia hết cho d
=>60n+5 chia hết cho d và 60n+4 chia hết cho d
=>1 chia hết cho d
=>d=1
=>PSTG

(a) \(A=\dfrac{3}{x-2}\in Z\)
\(\Rightarrow\left(x-2\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\\x=4\\x=-2\end{matrix}\right.\)
Vậy: \(x\in\left\{-2;0;2;4\right\}.\)
(b) \(B=-\dfrac{11}{2x-3}\in Z\)
\(\Rightarrow\left(2x-3\right)\inƯ\left(11\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\left[{}\begin{matrix}2x-3=1\\2x-3=-1\\2x-3=11\\2x-3=-11\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\\x=7\\x=-4\end{matrix}\right.\)
Vậy: \(x\in\left\{-4;1;2;7\right\}.\)
(c) \(C=\dfrac{x+3}{x+1}=\dfrac{\left(x+1\right)+2}{x+1}=1+\dfrac{2}{x+1}\in Z\Rightarrow\dfrac{2}{x+1}\in Z\)
\(\Rightarrow\left(x+1\right)\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x+1=1\\x+1=-1\\x+1=2\\x+1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\\x=1\\x=-3\end{matrix}\right.\)
Vậy: \(x\in\left\{-3;-2;0;1\right\}.\)
(d) \(D=\dfrac{2x+10}{x+3}=\dfrac{2\left(x+3\right)+4}{x+3}=2+\dfrac{4}{x+3}\in Z\Rightarrow\dfrac{4}{x+3}\in Z\)
\(\Rightarrow\left(x+3\right)\inƯ\left(4\right)=\left\{\pm1;\pm2\pm4\right\}\)
\(\Rightarrow x\in\left\{-2;-4;-1;-5;1;-7\right\}\)

a: |x+6|+2>=2
=>A<=1/2
Dấu = xảy ra khi x=-6
b: \(B=\dfrac{2+2\left|x+1\right|+1}{1+\left|x+1\right|}=2+\dfrac{1}{1+\left|x+1\right|}\)
|x+1|+1>=1
=>1/1+|x+1|<=1
=>B<=3
Dấu = xảy ra khi x=-1
c: 1945-|2x-9|<=1945
=>C<=1945/2015
Dấu = xảy ra khi x=9/2
d: -1/5|2y+6|<=0
=>D<=8
Dấu = xảy ra khi y=-3
e: |x-1|+60>=60
=>2014/|x-1|+60<=2014/60
=>E<=2014/60-1954/60=1
Dấu = xảy ra khi x=1

|-3,14|=3,14
|41|=41
|-5|=5
|1,(2)|=1,(2)
\(\left|-\sqrt{5}\right|=\sqrt{5}\)
\(\left|-\Pi\right|=\Pi\)

 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ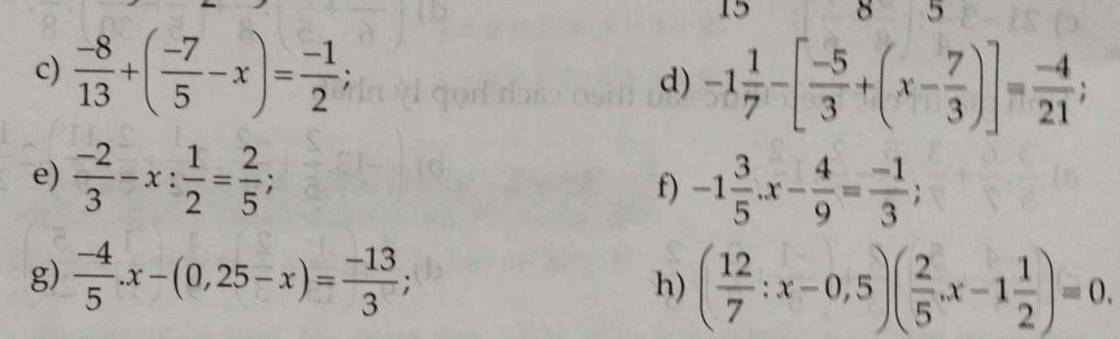
 giúp em với ạ em đang cần gấp ạ
giúp em với ạ em đang cần gấp ạ giúp em với ạ em đang cần gấp ạ :(
giúp em với ạ em đang cần gấp ạ :(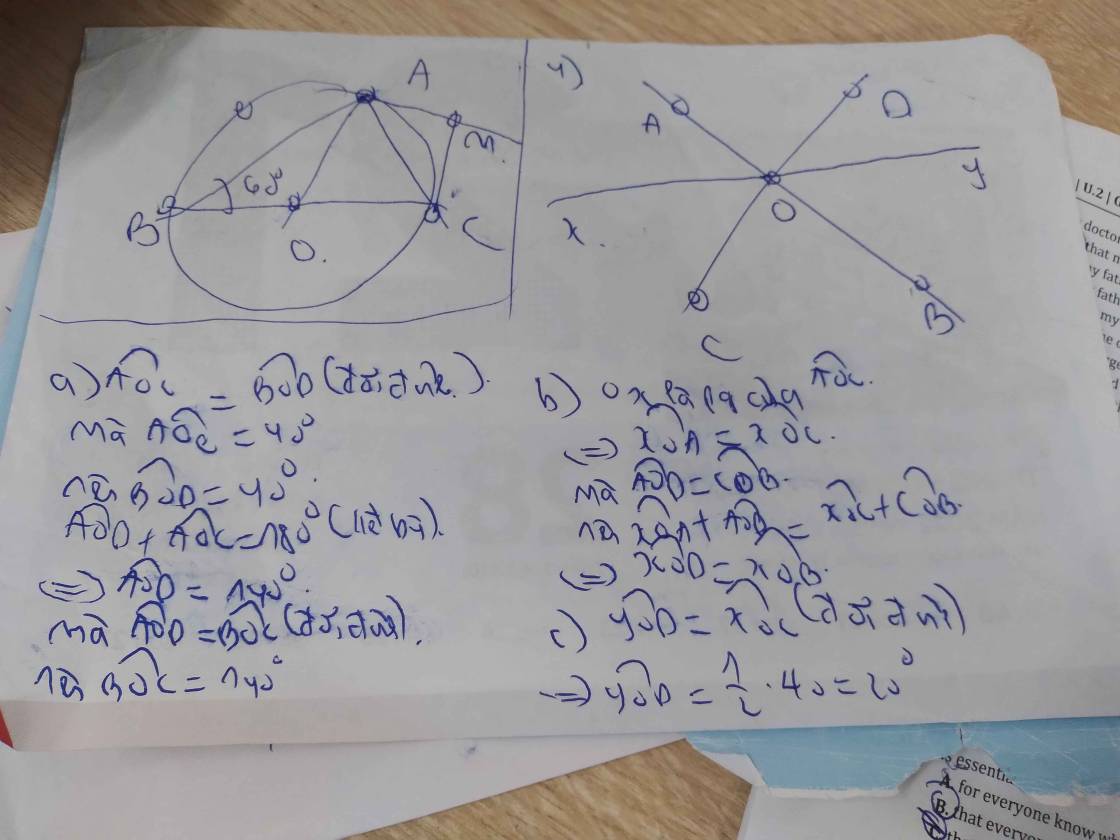

 giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước
giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước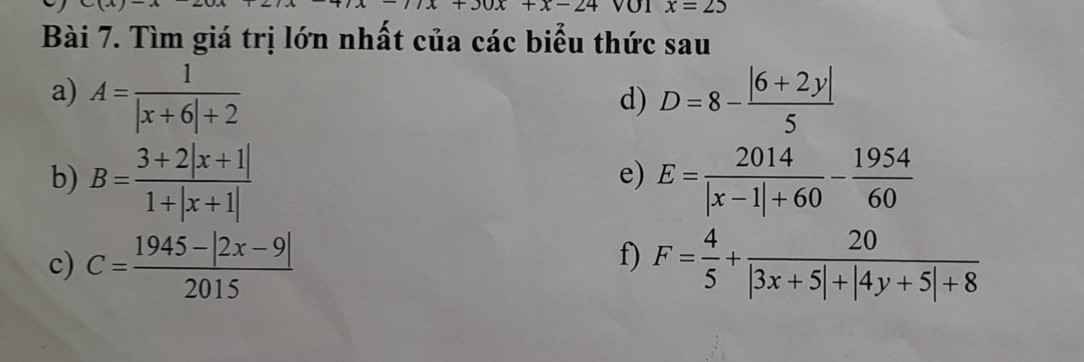
 giúp em với :( em cần gấp ạ
giúp em với :( em cần gấp ạ