Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng HTL: \(AH^2=BH\cdot HC=144\Rightarrow AH=12\left(cm\right)\)
\(BC=BH+HC=25\left(cm\right)\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot12\cdot25=150\left(cm^2\right)\)
Ta có \(\tan\widehat{HAB}=\dfrac{HB}{HA}=\dfrac{9}{12}=\dfrac{3}{4}\approx\tan37^0\)
Vậy \(\widehat{HAB}\approx37^0\)

Cái này là giải tam giác, em muốn làm được thì đọc lại lý thuyết về: Định nghĩa các giá trị lượng giác sin, cos, tam và cotan, về định lý Pita go và hệ thức lượng trong tam giác là có thể giải được :) Nếu em mới bắt đầu lên lớp 9 thì cô khuyên nên học hình cẩn thận ngay từ đầu vì nó sẽ khá khó ^^
Cô sẽ giúp bài này nhé :)
Xét tam giác vuông ABH, ta có: \(sinABH=\frac{AH}{AB}=\frac{2}{4}=\frac{1}{2}\)
Vậy góc B = 30 độ. Từ đó góc C = 60 độ.
Do góc B=30 độ nên \(cosB=\frac{BA}{BC}=\frac{4}{BC}=cos30=\frac{\sqrt{3}}{2}\)
Vậy \(BC=\frac{8\sqrt{3}}{3}\)
Từ đo có thể dùng Pitago hoặc định nghĩa lượng giác tìm \(AC=\frac{4\sqrt{3}}{3}\)

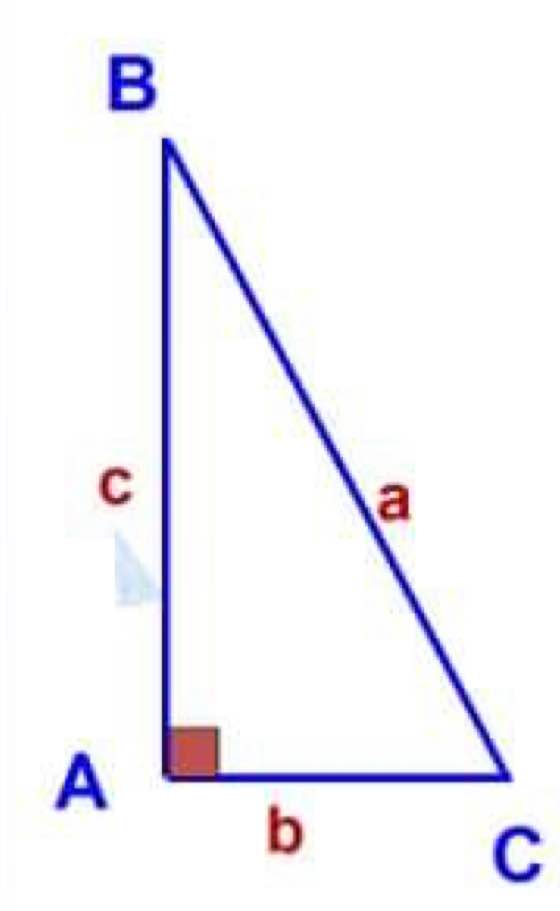
a: \(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}\)

cho tam giác abc vuông tại a biết ab=6cm,ac=8cm, a tính bc , b trên tia đối tia ac lấy điểm d sao cho ac=ad chứng minh tam giác bcd cân , c từ a vẽ ah vuông góc với bd tại h ak vuông góc bc tại k chứng minh tam giác bah= tam giác bka ,chứng minh tam giacs bhk cân từu đso chứng minh hk//cd , d qua điểm d kẻ đường thẳng a vuông góc vưới bd tại d qua điểm c kẻ đường thẳng b vuông góc với bc tại điểm c hai đường thẳng a và b cắt tại o chứng minh o,a,b thẳng hàng giúp mình với