K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên
MP
0


H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
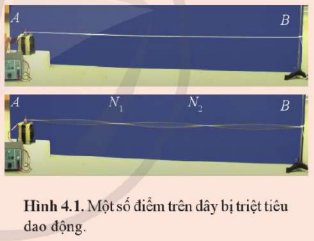
- Các điểm dao động với biên độ cực đại là bụng sóng.
- Các điểm không dao động (đứng yên) là nút sóng.
UN
0


MN
28 tháng 10 2017
khi đ1 và đ2 sáng bt thì
I = I đm = I1đm + I2đm ( 2 cái I này bạn tính ở từng đèn )
⇔ \(\dfrac{U}{R_{tđ}}\)= I đm = I1đm + I2đm
⇔\(\dfrac{U}{R_1+\dfrac{R_{đ2}.R_{đ1}}{R_{đ2}+R_{đ1}}}\) = I1đm + I2đm
thế số vô => R1