K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 8 2021
\(log_{\sqrt{x}}y=\dfrac{2y}{5}\Rightarrow2log_xy=\dfrac{2y}{5}\) \(\Rightarrow log_xy=\dfrac{y}{5}\)
\(log_{\sqrt[3]{5}}x=\dfrac{15}{y}\Rightarrow3log_5x=\dfrac{15}{y}\Rightarrow log_5x=\dfrac{5}{y}\)
\(\Rightarrow log_xy=\dfrac{1}{log_5x}=log_x5\Rightarrow y=5\)
\(\Rightarrow log_5x=\dfrac{5}{5}=1\Rightarrow x=5\)
\(\Rightarrow x^2+y^2=25+25=50\)
DD
Đoàn Đức Hà
Giáo viên
2 tháng 1 2023
\(f\left(x\right)=ax^3+bx^2+cx+d\)
Dựa vào đồ thị ta có: \(f\left(-2\right)=2,f\left(-1\right)=-1,f\left(0\right)=0,f\left(1\right)=-1\)
Từ đó suy ra \(f\left(x\right)=-x^3-x^2+x\).
\(g\left(x\right)=\left|f^3\left(x\right)-3f\left(x\right)\right|\)
\(h\left(x\right)=f^3\left(x\right)-3f\left(x\right)\)
\(h'\left(x\right)=3f'\left(x\right)f^2\left(x\right)-3f'\left(x\right)\)
\(h'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f^2\left(x\right)=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f\left(x\right)=1\\f\left(x\right)=-1\end{matrix}\right.\)
\(f'\left(x\right)=0\) có \(2\) nghiệm đơn
\(f\left(x\right)=1\) có \(1\) nghiệm đơn
\(f\left(x\right)=-1\) có \(1\) nghiệm đơn, \(1\) nghiệm kép.
Kết hợp lại ta được phương trình \(h'\left(x\right)=0\) có \(4\) nghiệm bội lẻ (do nghiệm \(x=-1\) vừa là nghiệm kép của \(f\left(x\right)=-1\) vừa là nghiệm đơn của \(f'\left(x\right)=0\)).
mà \(limh\left(x\right)=-\infty\) do đó \(g\left(x\right)=\left|h\left(x\right)\right|\) có \(3\) điểm cực đại, \(4\) điểm cực tiểu suy ra \(T=n^m=4^3=64\).
Chọn A.
AM
10 tháng 2 2022
Ta có: \(\int\dfrac{xdx}{x^2+3}\)
Đặt \(u=x^2+3\left(u>0\right)\)
Có \(du=2xdx\)
\(\Rightarrow\int\dfrac{xdx}{x^2+3}=\)\(\int\dfrac{du}{2u}=\dfrac{1}{2}ln\left(u\right)=\dfrac{1}{2}ln\left(x^2+3\right)\)
24 tháng 1
c: \(12\cdot3^x+3\cdot15^x-5^{x+1}=20\)
=>\(12\cdot3^x+3\cdot3^x\cdot5^x-5^x\cdot5-20=0\)
=>\(3^x\cdot3\left(5^x+4\right)-5\left(5^x+4\right)=0\)
=>\(\left(3^{x+1}-5\right)\left(5^x+4\right)=0\)
=>\(3^{x+1}-5=0\)
=>\(3^{x+1}=5\)
=>\(x+1=log_35\)
=>\(x=log_35-1\)
f: \(25^x-2\left(3-x\right)\cdot5^x+2x-7=0\)
=>\(\left(5^x\right)^2+5^x\cdot\left(2x-6\right)+2x-7=0\)
=>\(\left(5^x\right)^2+5^x\left(2x-7\right)+5^x+2x-7=0\)
=>\(5^x\left(5^x+2x-7\right)+\left(5^x+2x-7\right)=0\)
=>\(\left(5^x+1\right)\left(5^x+2x-7\right)=0\)
=>\(5^x+2x-7=0\)
Đặt \(A\left(x\right)=5^x+2x-7\)
=>\(A'\left(x\right)=5^x\cdot ln5+2>0\forall x\)
=>A(x) đồng biến trên R
=>A(x)=0 khi và chỉ khi x=1
i: \(9^x+2\left(x-2\right)\cdot3^x+2x-5=0\)
=>\(\left(3^x\right)^2+3^x\left(2x-5\right)+3^x+2x-5=0\)
=>\(\left(3^x+2x-5\right)\left(3^x+1\right)=0\)
=>\(3^x+2x-5=0\)
Đặt \(B\left(x\right)=3^x+2x-5\)
=>\(B'\left(x\right)=3^x\cdot ln3+2>0\)
=>B(x) luôn đồng biến trên R
=>B(x)=0 khi và chỉ khi x=1
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 2 2022
\(g'\left(x\right)=3.f'\left(3x\right)+9=0\Rightarrow f'\left(3x\right)=-3\Rightarrow\left[{}\begin{matrix}3x=-1\\3x=0\\3x=1\\3x=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=0\\x=\dfrac{1}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow\) Trên \(\left[-\dfrac{1}{3};\dfrac{1}{3}\right]\) hàm \(g\left(x\right)\) đạt cực đại tại \(x=0\) và cực tiểu tại \(x=-\dfrac{1}{3};\dfrac{1}{3}\)
\(\Rightarrow g\left(x\right)_{max}=g\left(0\right)=f\left(0\right)\)
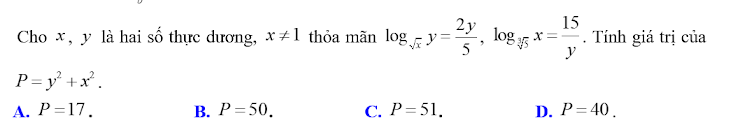
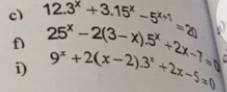
nhìn không rõ,chữ đẹp lên
cho chóp tam giácA.ABC có đáy là tam giác vuông tại B cạnh bên sa vuông với đáy, có SA = 2a, AB = a, BC= a\(\sqrt{3}\), gọi M là điểm trên cạnh SB sao cho 2SM=MB và N là trung điểm cạnh SC. tính thể tích của khối chóp A.MNCB