
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ:\(x>-3\)
\(\sqrt{x}+\sqrt{x+3}=x+4\)\(\Leftrightarrow x+x+3+2\sqrt{x}\sqrt{x+3}=\left(x+4\right)^2\)
\(\Leftrightarrow2x+3+2\sqrt{x^2+3x}=x^2+8x+16\)
\(\Leftrightarrow x^2+8x+16-2x-3-2\sqrt{x^2+3x}=0\)
\(\Leftrightarrow\left(x^2+3x-2\sqrt{x^2+3x}+1\right)+3x+12=0\)
\(\Leftrightarrow\left(\sqrt{x^2+3x}-1\right)^2+3\left(x+4\right)=0\)
Ta thấy:\(\hept{\begin{cases}\left(\sqrt{x^2+3x}-1\right)^2\ge0\\x>-3\Leftrightarrow3\left(x+4\right)>0\end{cases}}\)
\(\Rightarrow\left(\sqrt{x^2+3x}-1\right)^2+3\left(x+4\right)>0\)
\(\Leftrightarrow x\in\varnothing\)
Vậy phương trình vô nghiệm.

Tọa độ giao điểm A,B là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}x^2=2x+3\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-3\right)\left(x+1\right)=0\\y=2x+3\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(3;9\right);\left(-1;1\right)\right\}\)
vậy: A(3;9); B(-1;1)


Bài 1:
a: Xét tứ giác NPIK có
\(\widehat{NKP}=\widehat{NIP}\left(=90^0\right)\)
Do đó: NPIK là tứ giác nội tiếp
hay N,P,I,K cùng thuộc 1 đường tròn
b: Xét tứ giác MKHI có
\(\widehat{MKH}+\widehat{MIH}=180^0\)
Do đó: MKHI là tứ giác nội tiếp
hay M,K,H,I cùng thuộc 1 đường tròn

a: Δ=(m-2)^2-4(m-4)
=m^2-4m+4-4m+16
=m^2-8m+20
=m^2-8m+16+4
=(m-2)^2+4>=4>0
=>Phương trình luôn có 2 nghiệm pb
b: x1^2+x2^2
=(x1+x2)^2-2x1x2
=(m-2)^2-2(m-4)
=m^2-4m+4-2m+8
=m^2-6m+12
=(m-3)^2+3>=3
Dấu = xảy ra khi m=3

a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2

B A C H
\(\frac{AB}{AC}=\frac{5}{6}\)\(\Rightarrow\)\(\frac{AB}{5}=\frac{AC}{6}=x\) \(\left(x>0\right)\)
\(\Rightarrow\)\(AB=5x;\)\(AC=6x\)
Áp dụng hệ thức lượng ta có:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
\(\Leftrightarrow\)\(\frac{1}{9}=\frac{1}{25x^2}+\frac{1}{36x^2}\)
\(\Leftrightarrow\)\(\frac{61}{900x^2}=\frac{1}{9}\)
\(\Rightarrow\)\(900x^2=549\)
\(\Rightarrow\)\(x=\sqrt{\frac{549}{900}}=\frac{\sqrt{61}}{10}\)
\(\Rightarrow\)\(AB=\frac{\sqrt{61}}{2}\); \(AC=\frac{3\sqrt{61}}{5}\)
Áp dụng Pytago ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\) \(BC=61x^2\)
\(\Leftrightarrow\)\(BC=x\sqrt{61}\)
\(\Leftrightarrow\)\(BC=\frac{\sqrt{61}}{10}.\sqrt{61}=6,1\)
p/s: bạn tham khảo nhé, do số không đẹp nên có lẽ mk tính toán sai 1 số chỗ, bạn bỏ qua và ktra nhé, sai đâu ib mk

B A C H
\(\frac{AB}{AC}=\frac{5}{6}\)\(\Rightarrow\)\(\frac{AB}{5}=\frac{AC}{6}=x\) \(\left(x>0\right)\)
\(\Rightarrow\)\(AB=5x;\)\(AC=6x\)
Áp dụng định lý Pytago ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\)\(BC^2=61x^2\)
\(\Leftrightarrow\)\(BC=x\sqrt{61}\)
Áp dụng hệ thức lượng ta có:
\(AB.AC=AH.BC\)
\(\Leftrightarrow\)\(30x^2=3x\sqrt{61}\)
\(\Leftrightarrow\)\(x=\frac{\sqrt{61}}{10}\)
Đến đây bạn thay x vào các biểu thức tính AB,AC,BC ở trên nhé





 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
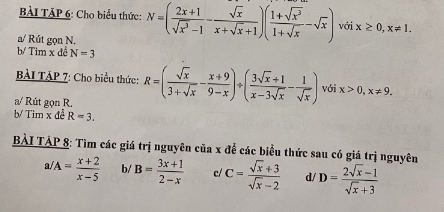 giúp em với, em đang cần bài này ạ
giúp em với, em đang cần bài này ạ